Graph Theory

Introducción:

Un grafo es un par $G = (V, E)$ de conjuntos tal que $E \subseteq [V]^2$; así, los elementos de $E$ son 2-elementos subconjuntos de $V$. Los elementos de $V$ son los vértices (o nodos, o puntos) del grafo $G$. Los elementos de $E$ son sus aristas (o líneas).

Nota:

La forma habitual de representar un grafo es dibujar un punto para cada vértice y unir dos de estos puntos con una línea si el correspondiente dos vértices forman una arista. Cómo se dibujan estos puntos y líneas es considerado irrelevante: lo único que importa es la información de qué pares de vértices forman una arista y cuáles no.

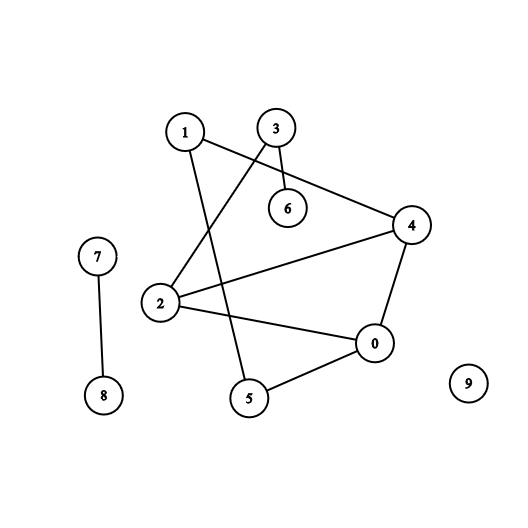
El grado de un vértice

Sea $G = (V, E)$ un grafo (no vacío). El conjunto de vecinos de un vértice $v$ en $G$ es denotado por $N_G(v)$, o susintamente por $N(v)$. Más generalmente por $U \subseteq V$, los vecinos en $V \setminus U$ de vértices $U$ son llamados vecinos de $U$; su conjunto es denotado por $N(U)$.

El grado $d_G(v) = d(v)$ de un vértice $v$ es la cantidad de vecinos de $v$ en $G$, numéricamente $\vert N(v)\vert$.

Proposición: El número de vértices con grado impar de un grafo es siempre par.

prueba: notemos por doble conteo que cada arista aporta con $2$ a la suma total de grados.

\[\sum\limits_{x \in V} d(x) = \sum\limits_{(x, y) \in E} 2 = 2 \cdot \vert E \vert \equiv 0 \mod 2\]

Por tanto, al ser la suma de grados par, necesariamente la suma de grados impares es par.

Caminos y Ciclos

Un camino es un grafo no vacío $P = (V, E)$ de la forma

\[V = \{x_0, x_1, \ldots , x_k \} ~~~~E=\{x_0x_1, x_1x_2,\ldots, x_{k-1}x_k\}\]

Donde los $x_i$ son todos distintos. Los vértices $x_0$ y $x_k$ son enlazados por $P$ y son llamados vértices finales o finales; los vértices $x_1, \ldots, x_{k-1}$ son los vértices internos de $P$. La longitud de un camino se define como la cantidad de aristas en $P$.

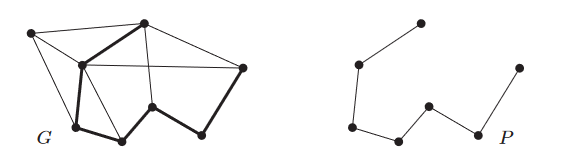
Si $P = x_0\ldots x_{k-1}$ es un camino con $k \ge 3$, entonces el grafo $C := P + x_{k-1}x_0$ es llamado un ciclo. La longitud de un ciclo es su número de aristas.

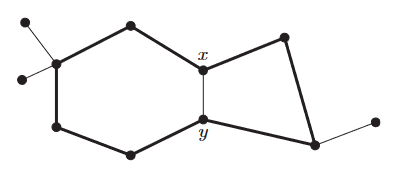
Ejemplo 1: Probar que todo grafo $G$ contiene un camino de longitud $\delta(G) = \min\limits_{v \in V} d(v)$. Además, si $\delta(G) \ge 2$ existe un ciclo de longitud al menos $\delta(G) + 1$.

prueba: Si tomamos un nodo $x_0 \in V$ arbitrario, y elegimos el camino más largo iniciando en $x_0$, con el otro nodo final $x_k$, necesariamente todos los vecinos de $u$ pertenecen a este camino $P_{x_0, x_k}$, en otro caso podría extenderse. Finalmente el nodo vecino más alejado de $x_k$, por el camino, es al menos $d(x_k) \ge \delta(G)$. Similarmente para formar un ciclo.

Conectividad:

Un grafo $G$ es llamado conexo si es no vacío y cualesquiera dos de sus vértices están enlazados por un camino en $G$. Dado $U \subseteq V[G]$, i.e. Un subconjunto del conjunto de vértices de G, y similarmente $W \subseteq E[G]$, se define $G[U, W]$ como un grafo de expansión de $G$, un grafo de expansión conexo maximal es denominado una componente conexa, todo grafo se puede particionar en una cantidad única de componentes conexas.

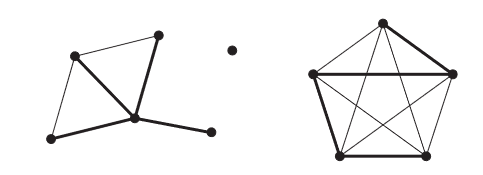
La imagen anterior representa un grafo con 3 componentes, además, en cada una de ellas se muestra una componente de expansión con mínima cantidad de aristas.

Representación de grafos:

Nosotros podemos escoger entre dos maneras estándar de representar un grafo $G$: Como una colección de listas de adjacencia o como una matriz de adjacencia. La cantidad de memoria que usa cada representación es $O(V + E)$ y $O(V^2)$, respectivamente.

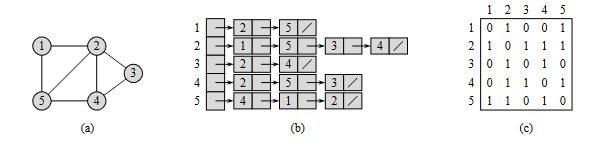
La representación por listas de adjacencia de un grafo $G$ consiste de un array Adj de $\vert V \vert$ listas (vectores), uno por cada vértice en $V$. Por cada $u \in V$, la lista de adjacencia Adj$[u]$ contiene todos los vértices $v$ tal que existe una arista $(u, v) \in E$.

vector<pair<int, int>> E = {{1, 2}, {1, 5}, {2, 3}, 
                            {2, 4}, {2, 5}, {3, 4}, 
                            {4, 5}};
vector<vector<int>> Adj(5 + 1);
for (auto [u, v] : E) {
    Adj[u].push_back(v);
    Adj[v].push_back(u);
}

La representación por matriz de adjacencia de un grafo $G$ consiste de una matriz $\vert V\vert\times \vert V\vert$ $A = \left(a_{i j}\right)$ tal que:

\[a_{ij} = \begin{cases} 1 & \text{si} ~(i, j) \in E, \\ 0 & \text{en otro caso.}\end{cases}\]

vector<pair<int, int>> E = {{1, 2}, {1, 5}, {2, 3}, 
                            {2, 4}, {2, 5}, {3, 4}, 
                            {4, 5}};
vector<vector<bool>> Adj(5+1, vector<bool>(5 + 1));
for (auto [u, v] : E) {
    Adj[u][v] = Adj[v][u] = 1;
}   

Preguntas:

Se define un grafo dirigido a un grafo donde hay una distinción entre la arista $(u, v)$ de la arista $(v, u)$. Un ejemplo es un la relación $a$ es padre de $b$. donde, si existe $(a, b) \in E$ implica que $(b, a) \notin E$. Para este tipo de grafos se define el grado de entrada in-degree y de salida out-degree para un nodo $v$, como la cantidad de aristas $(u, v)$ y $(v, u)$, respectivamente. Implemente un algoritmo para calcular el out-degree de cada nodo.
Pruebe que todo grafo $G$ con $\delta(G) \ge 2$, contiene un ciclo.
Pruebe que todo grafo $G$, tal que $\forall v \in V$ se cumple $d(v) \equiv 0 \mod 2$ tiene una partición de aristas por ciclos.
El cuadrado de un grafo $G = (V, E)$ es el grafo $G^2 = (V, E^2)$ tal que $(u, v) \in E^2$, si y solo si, $G$ contiene un camino de longitud $2$ desde $u$ hasta $v$. Hallar para las representaciones standard el cuadrado de un grafo.
Diseñe un algoritmo que en tiempo $O(V)$ decida si existe una fuente universal -Un nodo con in-degree $\vert V\vert-1$ y out-degree $0$.-
Sea $G$ un grafo conteniendo un ciclo $C$, y asume que $G$ contiene un camino de longitud al menos $k$ entre dos vértices de $C$. Muestre que $G$ contiene un ciclo de longitud al menos $\sqrt k$.
Mostrar que todo grafo conexo $G$ contiene un camino o un ciclo de longitud al menos $\min \left(2\delta(G), \vert G \vert \right)$.

Reconocimiento de Componentes (intro. a DFS):

Supongamos que dado un grafo $G = (V, E)$ queremos reconocer sus componentes, i.e. Aquellos conjuntos conexos maximales.

En primer lugar, es claro que las componentes son únicas ya que la relación de conexidad es de equivalencia. Por tanto, si tomamos un nodo $v$ arbitrario, todos los nodos $u$ conectados a el, en general todos los nodos de la componente de $v$, estan relacionados a un camino $P_{v, u}$. Si generamos todos los caminos desde un nodo arbitrario $v$, el conjunto de todos los nodos finales de esos caminos, serán igual a los nodos de la componente de $v$.

Todos los caminos de un grafo:

Dado un nodo arbitrario $v$, cada camino empezando en $v$ es una sucesión de aristas, i.e elección de un nodo vecino. Cumpliendo la restricción que ningún número se debe repetir. Formularemos el siguiente algoritmo:

Comenzamos con un nodo $v$ y el camino $P_{v, v}$.
Buscamos una arista desde el final del camino que no se haya visto:
1. Si existe, agregamos la arista al camino.
2. En otro caso, eliminamos del grafo la ultima arista usada.
Si existe arista en $G$, regresar a (2).

Notemos que este, en práctica es un proceso enumerativo, cuenta la cantidad de caminos empezando en cada configuración de aristas.

vector<bool> in_path; //size = n
void all_path(int v) {
    in_path[v] = true;
    for (int u : Adj[v]) {
        if (in_path[u]) continue;
        all_path(u);
    }
    in_path[v] = false;
}

Una solución menos eploxiva:

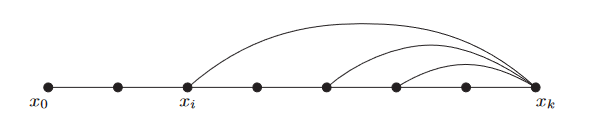
Notemos que la cantidad de veces que consideramos un final, puede ser muy grande.

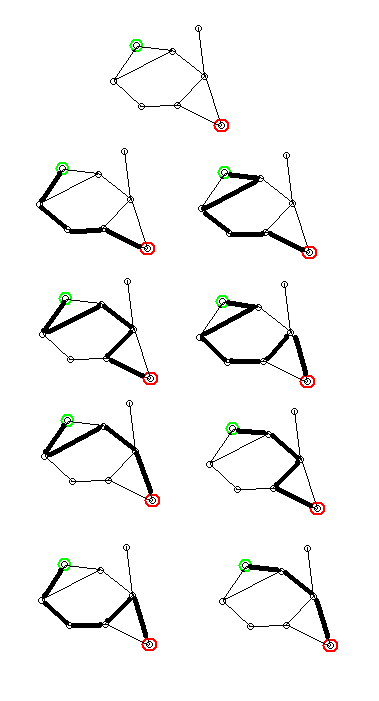
La imagen muestra que la cantidad de veces que consideramos un final puede ser grande. Sin embargo, ¿necesitamos visitar tantas veces un nodo?

No, Solo necesitamos contar la primera vez que encontramos un nodo, ¿Por qué?.

Supongamos que no llegamos a encontrar todos los nodos, sea $u$ uno de ellos y por tanto existe un camino $P_{v, u}$ donde al menos se ha descubierto el nodo $v$. Sea el primero nodo $w$ en el camino desde $v$ a $u$ que tampoco fue encontrado, obviamente el nodo anterior a ese en el camino existe y ha sido encontrado por el algoritmo. Por tanto, como ese nodo reviso todas sus aristas, debió considerar a $w$ en su búsqueda, lo cual es una contradicción.

Código para hallar componentes:

vector<bool> encontrado; //size = n
vector<int> color; //size = n
void dfs(int v, int comp_id) {
    encontrado[v] = 1;
    color[v] = comp_id;
    for (int u : g[v]) {
        //me aseguro si ya ha sido 
        //encontrado (primera vez)
        if (encontrado[u]) continue;
        dfs(u, comp_id);
    }
}

//se asume que los nodos son 0, 1, ..., n-1
void colorear_componentes() {
    int comp = 0;
    for (int i = 0; i < n; ++i) {
        if (color[i] != 0) continue;
        //cada componente es enumerada
        //segun el orden en que se encontró
        dfs(i, ++comp);
    }
}

Complejidad:

Basta usar la siguiente información: como cada nodo es visitado una sola vez, esto quiere decir que sus aristas vecinas son consideradas una sola vez. Por tanto, la complejidad debe ser: $O(\vert V\vert + \vert E\vert)$, visitamos cada arista $2$ veces, pero la complejidad absorbe las constantes.

Problemas:

Written on January 14, 2022