Árboles y Bosques

Un grafo acíclico, aquel que no contiene ciclos, es llamado un bosque. El bosque conexo se llama árbol. (Así, un bosque es un grafo cuyos componentes son árboles.) Los vértices de grado $1$ en un árbol son sus hojas, los otros son sus vértices interiores. Cada árbol no trivial tiene una hoja, considere, por ejemplo, los extremos del camino más largo. Este pequeño hecho viene a menudo útil, especialmente en pruebas de inducción sobre árboles: Si quitamos una hoja de un árbol, lo que queda sigue siendo un árbol.

Teorema 1:

Lo siguientes afirmaciones son ciertas para cada grafo T.

1. $T$ es un árbol;
2. Cualesquiera dos vértices en $T$ están unidos por un único camino en $T$;
3. $T$ es mínimamente conexo, i.e. $T$ es conexo pero, $T - e$ es disconexo para toda arista $e \in T$;
4. $T$ es máximamente acíclico, i.e. $T$ no contiene ciclos pero $T + (x, y)$ sí, para cualesquiera dos vértices no adyacentes $x, y \in T$.

Prueba:

$1 \Rightarrow 2$. Supongamos que existen más de un camino entre los nodos $u, v \in T$. Sean $x_0, x_1, \ldots, x_k$ y $y_0, y_1, \ldots, y_m$ dos caminos distintos entre $u$ y $v$. Sea $a$ el anterior nodo a los primeros nodos distintos entre los dos caminos y $b$ el siguiente nodo en comun entre los caminos después de $a$. Vemos que entre $a$ y $b$ existe un ciclo. Contradicción.

$2 \Rightarrow 3$. Sea $e = (u, v)$ una arista de $T$, como $e$ es el único camino entre $u$ y $v$. entonces $T-e$ desconecta $T$.

$2 \Rightarrow 4$. Si existe un ciclo en $T$, entonces, hay dos caminos entre los nodos del árbol, lo cual es una contradicción. Por otro lado, si agregamos una arista entre dos nodos no adyacentes, vemos que formamos un ciclo.

$3 \Rightarrow 1$. Si $T$ contiene un ciclo $x= z_1, \ldots, z_k=y$, entonces $T - e$ es aun conexo, como en cualquier paseo $u-v$ la arista $\left(x, y\right)$ puede ser reemplazado por el camino $z_1, z_2, \ldots, z_k$. Como contradice la minimalidad de $G$, concluimos que $G$ es acíclico, y por lo tanto un árbol.

$4 \Rightarrow 1$. Si $x, y \in T$ están en distintas componentes no se puede crear un ciclo al agregar la arista $\left(x, y\right) \in E$, Así $T$ es un árbol.

Corolario

Un grafo conexo con $n$ vértices es un árbol si y solo si tiene $n-1$ aristas.

Raíz de un árbol

A veces es conveniente considerar un vértice de un árbol como especial; tal vértice es llamado raíz del árbol. Un árbol $T$ con una raíz fija es un árbol enraizado. De esta forma se define un orden parcial sobre los nodos, que llamaremos altura. Un vértice a una distancia $k$ de la raíz forma parte del $k$-ésimo nivel del arbol enraizado.

Corolario 2:

Todo grafo conexo contiene un árbol de expansión, que es, un árbol conteniendo todos los vértices del grafo.

prueba:

Tomar el minimo subgrafo conexo de expansión.

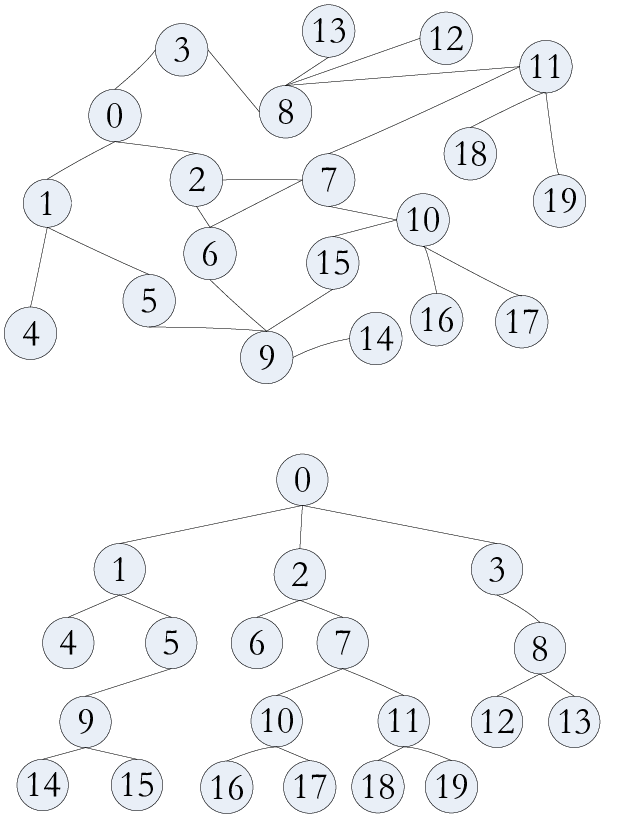
Breadth-first search (BFS)

Dado un grafo $G = (V, E)$ y un vértice fuente $s$, se explora sistemáticamente las aristas de $G$ para “descubrir” cada vértice que es accesible desde $s$. Calcula la distancia (menor número de aristas) desde $s$ a cada vértice alcanzable. También produce un “BFS-Tree” con raíz $s$ que para cualquier vértice alcanzable desde $s$, el camino simple en el BFS-Tree de $s$ corresponde a un “camino más corto” de $s$ en $G$, es decir, un camino que contiene el menor número de aristas.

El algoritmo funciona tanto en grafos dirigidos como no dirigidos. Es decir, el algoritmo descubre todos los vértices a distancia $k$ de $s$ antes de descubrir cualquier vértices a distancia $k + 1$.

Para realizar un seguimiento del progreso, el BFS colorea cada vértice de blanco, gris o negro. Todos los vértices comienzan siendo blancos y luego pueden volverse grises y entonces negros. Un vértice es descubierto la primera vez que es encontrado durante la búsqueda, momento en el cual se vuelve no blanco. Vértices gris o negros, por tanto, son vértices descubiertos, pero en la búsqueda se distingue entre ambos. Si $(u, v) \in E$ y el vértice $u$ es negro, entonces $v$ es entre gris o negro; que es, todos los vértices adyacentes para un vértices negro ha sido descubierto. Vértices grises pueden tener vecinos blancos; ellos representan la frontera entre vértices descubiertos y no descubiertos.

El BFS construye un árbol primero en anchura, que inicialmente contiene solo su raíz, que es el vértice de origen $s$. Cada vez que la búsqueda descubre un vértice blanco $v$ en el transcurso de escanear la lista de adyacencia de un vértice ya descubierto $u$. El vertice $v$ y la arista $(u, v)$ son agregadas al árbol. Decimos que $u$ es el predecesor o padre de $v$ en el BFS-Tree. Como un vértice es descubierto a lo más una vez, este tiene a lo más un padre. Relaciones de ancestros y descendientes en el BFS-Tree son definidas relativas al nodo raíz $s$: Si $u$ esta sobre el camino simple del árbol desde $s$ hacia $v$, entonces $u$ es ancestro de $v$ y $v$ es descendiente de $u$.

El siguiente código expresa el proceso BFS:

vector<int> color, d, pi;
void bfs(int s, vector<vector<int>>& g) {
    color[s] = 1;
    d[s] = 0;
    queue<int> Q;
    Q.push(s);
    while (!Q.empty()) {
        int u = Q.front();
        Q.pop();
        for (int v : g[u]) {
            if (color[v] == 0) {
                color[v] = 1;
                d[v] = d[u] + 1;
                pi[v] = u;
                Q.push(v);
            }
        }
        color[u] = 2;
    }
}

void init(int n) {
    color.assign(n, 0);
    d.assign(n, inf);
    pi.assign(n, -1);
}

El algoritmo trabaja como sigue. Con la excepción del vértice fuente $s$ se inicializa todos los nodos con color blanco y distancia actual infinito, así como padre desconocido. Se encola el vértice $s$. El bucle while trabaja como sigue: La primera línea manetiene los nodos grises descubiertos, aunque no se ha revisado su lista de adyacencia. Se mantienen las siguientes invariantes:

• La condición asegura que haya vértices grises descubiertos.
• La siguiente línea encuentra uno de estos vértices grises y se elimina de la cola para ser examinado.
• El bucle for busca vértices blancos en la lista de adyacencia de $u$.
• Al ser descubierto un nodo blanco, se pinta de gris, se calcula su distancia y su padre en el árbol.
• Al examinar todos los vértices de $u$, el nodo es marcado como negro.

El algoritmo de BFS puede retornar distintos árboles BFS, y descubrir los nodos en un orden distinto, pero los valores $d$ siempre serán los mismos.

Caminos más cercanos:

En primer lugar, afirmamos que nosotros encontramos distancias a todos los nodos alcanzables desde $s$ en $G$. Definimos la distancia mínima $\delta(s, v)$ desde $s$ hacia $v$ como la menor cantidad de aristas de un camino desde $s$ hacia $v$.

Lema 3:

Sea $G = (V, E)$ un grafo, y sea $s \in V$ arbitrario. Entonces, para cualquier arista $(u, v) \in E$.

Prueba:

Si $u$ es alcanzable desde $s$, entonces tambien $v$. En este caso, el camino más corto desde $s$ a $v$ no puede ser más grande que el camino más corto hacia $u$ seguido por la arista $\left(u, v\right)$, y así la inecuación cumple. Si $u$ no es alcanzable desde $s$, entonces $\delta\left(s, u\right) = \infty$ y cumple igualmente.

Lema 4:

Sea $G$ un grafo, y supongamos que el algoritmo BFS es ejecutado con un nodo $s$. Al terminar, cada vértice $v \in G$ satisface $d\left(v\right) \ge \delta(s, v)$.

Prueba:

Usaremos inducción sobre el número de encolamientos. Nuestra hipótesis inductiva es que $d\left(v\right) \ge \delta(s, v)$ para todo $v \in G$.

La base de la inducción es la situación inmediata despues de encolar $s$ antes del bucle while. En este momento la hipótesis cierra para todos los nodos.

Para el paso inductivo, consideramos un vértice blanco $v$ que es descubierto al buscar los vecinos de un vértice $u$. Sabemos que $d\left(u\right) \ge \delta\left(s, u\right)$. Del lema anterior y la asignación en el algoritmo tenemos:

Además, este vértice nunca más es encolado. Así se mantiene invariante la hipótesis para ese nodo en adelante.

Lema 5:

Supongamos que durante la ejecución del BFS sobre un grafo $G$, la cola $Q$ contiene los vértices ${v_1, v_2, \ldots, v_r}$, donde $v_1$ es el frente de la cola y $v_r$ la parte trasera. Entonces, $d(v_r) \le d(v_1) + 1$ y $d(v_i) \le d(v_{i+1})$ para todo $i = 1, 2,\ldots, k-1$.

Prueba:

La prueba es hecha por el número de usos de la cola. Inicialmente, cuando la cola contiene solo el nodo $s$, cumple trivialmente.

Si $v_1$ es desencolado, $v_2$ es el nuevo frente (Si la cola se queda vacía cumple trivialmente). Por la hipótesis de inducción $d(v_1) \le d(v_2)$. Pero entonces tenemos $d(v_r) \le d(v_1) + 1 \le d(v_2) + 1$, y las otras restricciones se mantienen.

Cuando encolamos un nodo $w$, este se vuelve $v_{r+1} = w$. En ese tiempo, ha sido removido el vértice $u$, y por la hipótesis inductiva, el nuevo frente $v_1$ cumple $d(v_1) \ge d(u)$. Así, $d(v_{r+1}) = d(w) = d(u) + 1 \le d(v_1) + 1$. Además, $d(v_r) \le d(u) + 1$, y así $d(v_r) \le d(u) + 1 = d(w) = d(v_{r+1})$, y así las restricciones se mantienen. Lo que termina de probar el enunciado.

Corolario

Supongamos dos vértices $u$ y $w$ encolados durante la ejecución del algoritmo, y $u$ es encolado antes de $w$. Entonces $d(u) \le d(w)$ en todo momento.

Teorema de correctitud del BFS

Sea $G$ un grafo y supongamos que el algoritmo BFS es ejecutado desde un vértice $s$. Se cumple que $d(v) = \delta(s, v)$ para todo $v \in G$; y un camino mínimo hacia todo nodo $u$ termina en la arista $(pi(u),u)$.

Prueba:

Asumamos, por el propósito de contradicción, que algún vértice no recibe un valor $d$ correcto. Sea aquel con mínimo $\delta(s, v)$ que recibe un valor incorrecto, claramente $v \neq s$. Por el lema $4$, $d(v) \ge \delta(s, v)$, y así $d(v) > \delta(s, v)$. El vértice $v$ debe ser alcanzable desde $s$, por si no lo es, entonces $\delta(s, v) = \infty \ge d(v)$. Sea $u$ el vértice immediatamente predecesor de $v$ sobre el camino más corto desde $s$ a $v$, tal que $\delta(s, v) = \delta(s, u) + 1$. Porque $\delta(s, u) < \delta(s, v)$, y de porque nosotros escogemos $v$, tenemos $d(u) = \delta(s, u)$. Uniendo estas propiedades juntas, tenemos:

Ahora consideremos el tiempo cuando el BFS escoje desencolar el vértice $u$. En este tiempo, el vértice $v$ tiene cualquiera de los colores. Si $v$ es blanco, entonces $d(v) = d(u) + 1$, contradiciendo la desigualdad de arriba. Si $v$ es negro, entonces ya fue removido desde la cola, por tanto $d(v) \le d(u)$, otra vez entrando en una contradicción. Si $v$ es gris, entonces este fue pintado gris luego de descubrir un vértice $w$. que ha sido removido antes de $u$ por lo cual $d(v) = d(w) + 1$. Sin embargo, $d(w) \le d(u)$, así tenemos $d(v) = d(w) + 1 \le d(u) + 1$, y otra vez se llega a una contradicción.

Finalmente, concluimos que $d(v) = \delta(s, v)$ para todo $v \in V$. Todos los vértices alcanzables desde $s$ debería ser descubiertos, en otro caso tenemos $d(v) > \delta(s, v)$. Para concluir la prueba del teorema, observamos que si $pi(v) = u$, entonces $d(v) = d(u) + 1$. Así, podemos obtener el camino más corto desde $s$ hasta $v$ tomando el camino más corto desde $s$ a $u$ agregando la arista $(pi(v), v)$.

Árbol BFS

Podemos ver que todos los nodos $v \in V$, excepto $s$, tiene un único nodo $pi(v)$, y así en total $\vert V\vert - 1$ aristas y, por tanto, forma un árbol.

Camino más corto

void imprimir_camino(vector<vector<int>>& G, int s, int v) {
    if (v == s)
        cout << s << endl;
    else if (pi[v] == -1)
        cout << "camino no valido" << endl;
    else {
        imprimir_camino(G, s, pi[v]);
        cout << v << endl;
    }
}