Problem A - Animal Farm

Statement Summary

Given an $n \times m$ matrix in which each cell might have walls in each direction (up, down, left, right), we consider that two cells are adyacent if they share a side and there is no wall on it. A region is a set of cells such that they are directly or indirectly adyacent. Considering that the cells outside the matrix belong to the same region, compute the number of different regions among the cells in the matrix.

Solution

To solve this problem we can build a graph in which two adyacent cells have an edge between them. Since the graph will have $nm$ nodes and at most $4nm$ edges, we can use any algorithm that computes connected components and a set to solve it in $O(nm\log{(nm)})$.

Problem B - Sleeping Baker

Statement Summary

Given an $n \times m$ binary matrix, compute the number of submatrices with side length greater than one and with ones at their corners

B.1. valid submatrices of the given example.

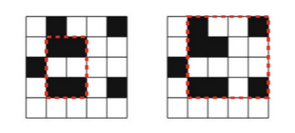
Solution

We can compute for each pair of distinct columns the number of 1s in common in each row. For every number $r$ of ones in common we add $\binom{r}{2}$. Using machine operations like with bitset we can speed up to $O(\frac{m^2n}{64})$ with a 64-bit compiler in this case.

Problem C - Card Testing

Statement Summary

Given some values for an XML file, you must print the corresponding format following some conditions.

Solution

This solve this problem we only need to implement some parsing function and do what the problem asks.

Problem D - Distributing Pizza

Statement Summary

Given a cyclic array of length $k$, we want to partition it into $n$ subarrays in such a way that the difference between the minimum and maximum sum in each subarray is minimal. Array elements are positive.

Solution

We can get a first complexity of $O(nk^7)$. We rotate in $O(k)$, we set the minimum and maximum sum in $O(k^4)$, finally we check with DP in $O(nk^2)$ if it is possible to make a valid partition.

With a two-pointer approach, we can reduce the DP to $O(nk)$, since the values ​​are all positive and we are only looking in a continuous range.

for (int i=0; i<=n; ++i) dp_acc[i][0] = 1;
for (int j=1; j<=k; ++j) {
    int l=-1,r=-1;
    for (int i=1; i<=n; ++i) {
        while (l+1 < i && s[i] - s[l+1] > R) l++;
        while (r+1 < i && s[i] - s[r+1] >= L) r++;
        if (r <= -1) dp[i][j] = 0;
        else if (l == -1) dp[i][j] = dp_acc[r][j-1] > 0;
        else dp[i][j] = dp_acc[r][j-1] > dp_acc[l][j-1];
    }
    for (int i=1; i<=n; ++i) {
        dp_acc[i][j] = dp[i][j] + dp_acc[i-1][j];
    }
}

On the other hand, by setting the minimum sum $L$ and maximum sum $R$ and verifying that $\left(L, R\right)$ is possible, then so is $\left(L, R+1\right )$ and $\left(L-1, R\right)$. The latter allows us to use two pointers, since the respective $R$ for each $L$ is a non-decreasing function $f$. Reducing an $O(k^4)$ to $O(k^2)$.

Finally, to get a complexity of $O(nk^3)$, instead of setting the rotation before setting the limits, because the array is cyclic we can decide that the maximum set sum occurs as a range at the beginning of our rotation.

int ans = infty;
for (int i=0, j=0; i<sums.size(); ++i) {
    while (j<sums.size() && !check(sums[i].value, sums[j].value, sums[j].l)) 
        j++;
    if (j==sums.size()) break;
    ans = min(ans, sums[j].value - sums[i].value);
}

Problem E - Engraved Stones

Statement Summary

Given two integer sequences $a$ and $b$ of length $n$, we must find the longest sequence $s$ such that $s$ can be obtained from both $a$ and $b$ by deleting some (posibly none) characters at the beginning and at the end of them.

Solution

This is the classical Longest Common Substring problem, which can be solved using Suffix Automaton in $O(n)$ (because the integer values belong to $[1, 100]$) or Suffix Array in $O(n\log{n})$.

To solve it with Suffix Array, we can compute the Suffix array ($SA$) and LCP array ($LCP$) over the string $T = a + sep_{1} + b + sep_{2}$ (where $sep_{1}$ and $sep_{2}$ are different characters that don’t appear neither in $a$ or $b$). Then, for each position of $T$ that corresponds to $a$/$b$ we should assign it the color $1$/$2$. The answer will be the maximum value of $LCP[i]$ such that $SA[i]$ and $SA[i + 1]$ are of different colors.

To learn how compute it with Suffix Automaton, you can check this tutorial

Problem F - Flip

Statement Summary

Given a $3 \times 3$ board with white and black cells, in one flip, the flipped cell and its side-adyacent cells change their color to the opposite one. Compute the minimum number of flips needed to change all the cells to white color.

Solution

To solve this problem, we can just brute force the choice of flipping each possible cell ($2^{9}$ possibilities) and then minimize the number of flips

Problem G - Game of Baker

Statement Summary

Given a pile with $N$ snacks, there are two players that take turns alternately. In one turn, the active player can eat between $1$ and $\min{\lbrace N, M\rbrace}$ from the pile. Then:

• If the pile is empty after the active player eats, then he wins.
• If the number of snacks remaining in the pile (counted in binary) contains an odd number of ones, then the active player loses.

You must check if the second-turn player wins or not if both players play optimally.

Solution

This problem can be solved by using dynamic programming for game theory:

Define $memo[i]$ as $1$ if the active player would win and $0$ otherwise.

Then, we must establish some conditions:

• If $i$ has an odd number of ones in its binary representation, then $memo[i] = 1$, since this would mean that the last active player lost.
• If $i = 0$, then $memo[i] = 0$, since the last active player won.
• Else, if there is at least one $0$ in the positions $[i - M, i - 1]$, then $memo[i] = 1$, otherwise $memo[i] = 0$.

We could mantain an extra array $prefix[i]$ such that it contains the sum of $memo[0] + \cdots + memo[i]$ and then compute the number of ones in any range in $O(1)$.

However, due to the memory limit, we are not allowed to declare $memo$, which forces us to think in a more elegant solution: Instead of computing the arrays $memo$ and $prefix$, we only care about the last $0$ registered, since we can check if there is at least one $0$ in $[i - M, i - 1]$ by comparing the position of the last zero with $i - M$: If it’s less than $i - M$, then there isn’t any, otherwise there is at least one.

This reduces our memory usage to $O(1)$ and our complexity will be $O(N)$.

Problem H - Hidden Number

Statement Summary

Given a sequence of $N$ coins, not necessarily different, you’re required to compute the minimum positive value that cannot be formed with a subset of them in such a way that each coin can be used only once and they are not divisible.

Solution

Note that if $1$ is not in my set, the answer is obviously $1$.

On the other hand, if I have $k$ coins with a value of $1$ and a coin with a value of $d \le k+1$, it’s like we had $k + d$ coins of value $1$, this means that any value between $1$ and $k+d$ can be formed.

Therefore, if we process the coins in order we can include new coins and “transform” them into $1$ coins. So the first time we have $k$ coins and a following coin $d$ with $d > k+1$ (assuming we add coin with infinite value), then we won’t be able to form the value $k+1$.

Problem I - Inserting Ominoes

Statement Summary

Given an image pattern and a board that consist of black and empty cells, we need to check if the given pattern could fit into the board in a way that no black cell from the pattern is put over another black cell or outside the board. We are allowed to rotate or flip the pattern any number of times.

Solution

To solve this problem we can just brute force each possible rotation and flip of the pattern and then check if the image fits or not using naive pattern searching. Since there will be a small number of different configurations, it will fit in the time limit.

Problem J - Jaime’s Room

Statement Summary

Given $n$ objects that are inside a room and $C$ boxes, we will receive $q$ queries that can be:

• m $i$ $j$ $k$: Put all the objects with ID between $i$ and $j$ in box $k$.
• b $k$: Throw box $k$ in the trash with all its contents.
• d $i$: Answer the label of the box that contains the object $i$.
• s $i$ $j$: Check if the objects $i$ and $j$ are in the same place.

Solution 1 (sqrt decomposition):

We use the typical sqrt decomposition approach of dividing our array into blocks of size $B$, with a lazy tag if we need to update the color, a special value for each index if it has been removed, and its respective color otherwise. Also, each range has a color sorted list, which is not necessarily available when you have the lazy tag enabled.

If we want to find the color of an index, it would be enough for us to first check if it has been eliminated, if not, if its block has the same color and finally its assigned color.

In case of updating a color in a range, fully included ranges will only change their lazy tag, otherwise we can change the colors and keep the list sorted in $O(B)$, using a merge with two pointers.

To eliminate a color we just have to go through each range and if it doesn’t have the lazy tag activated we can find the range to eliminate in the ordered list in $O(\log B)$, in case of having the lazy tag activated, we can go through the range and remove the colors, note that removing in this way only happens once per range.

Therefore, the cost we want to minimize is $B + \frac{n}{B} \log B$. whose optimal value for $n = 100000$ is $B \sim 942$.

Solution 2 (Amortized Analysis)

Let’s consider that we get rid of the deletion query ($b$ $k$), then this is a trivial problem that can be solved in $O(n\log{n})$ using sets and intervals for ranges that are inside the same box. However, to add the deletion query we must notice that an object in the box $k$ is in the trash if:

• The box $k$ was removed.
• It was thrown to the trash when it was inside a previous box. However, we won’t really delete objects (since that would affect the complexity), we will only mark them as removed.

For the first condition, we can mantain a set of removed boxes and just check if $k$ is inside it in $O(\log{n})$.

For the second condition there si some subtle observation: The object was put in box $k$ after it was in some box $x$. This means that we must modify the range assigning operation to mark each position as removed while iterating over the affected intervals. To do it we can use Fenwick Tree and prefix sums in a way that the position $i$ will be assigned to the number of times it was marked as removed, even if we only care about removing it once.

Finally, the complexity will be $O(q\log{n})$

Problem K - Keep the Order

Statement Summary

Given $t$ values of $n$; for each of them, compute the number of permutations of $1, 2, \ldots, n$ such that if we pick three different positions $i < j < k$, it doesn’t hold that $p_{i}$ is the minimum, $p_{j}$ is the maximum and $p_{k}$ is the medium one.

Solution

This problem asks us to compute the 132-avoiding permutations, which are related to the Catalan Numbers. How? Let’s see:

Let’s consider that we will fix the position $i$ of the maximum element $n$ to compute $f_{n}$, then we will have to assign $i - 1$ elements to its left and $n - i$ elements to its right. However, if we choose some position $l$ to its left and some position $r$ to its right, then it shouldn’t hold that:

But since $p_{i}$ is the maximum value, we only care about the first inequality (since the second one will hold anyways):

But since $l$ and $r$ are arbitrary, in particular:

Which means that we should assign the values in range $[n - i + 1, n - 1]$ to the left and the other values to the right in a valid way ($f_{i - 1}$ and $f_{n - i}$).

Now, we can fix $i$ as $1, 2, \ldots, n$, so we get the following recursion:

Which is equivalent to the computation of the $n$-th Catalan number.

Thus, we only need to compute the $n$-th Catalan number for each $n$ given. This can be computed in $O(n)$ using the recurrence:

And to avoid implementing the BigInteger class we can use Python.

Problem L - Lowest Risk Factor

Statement Summary

Given $q$ pairs $(n, k)$, for each pair we must compute the size of the following set:

Solution

To solve this problem we can preprocess the maximum prime factor for each integer between $2$ and $10^{5}$ (Max $n$ value) and solve the problem offline.

We will mantain $values[x]$ as the vector of all the integers that have $x$ as their maximum prime factor, so we can sort the queries by $k$ and do a line sweep to update and compute the answer for each of them (Initially all the positions will have a $0$ and then we will assign them $1$ when they are active). We will use a Fenwick Tree to help us query the number of valid integers.