Clase 02: Complejidades + STL
Leonidas
09-01-2020
¿ Cómo podriamos determinar cuánto demorará el siguiente programa (aproximadamente) para cualquier valor de n ?
vector <bool> sieve (int n) {
vector <bool> is_prime(n, true);
is_prime[0] = is_prime[1] = false;
for (int i = 2; i < n; i++) {
if (!is_prime[i]) continue;
for (int j = i + i; j < n; j += i) {
is_prime[j] = false;
}
}
return is_prime;
}Podemos tomar el tiempo que demora en ejecutar para distintos valores de n:
| n | time(s) |
|---|---|
| 1000000 | 0.099296 |
| 1100000 | 0.092526 |
| 1200000 | 0.098912 |
| 1300000 | 0.108183 |
| 1400000 | 0.118805 |
| 1500000 | 0.121858 |
| 1600000 | 0.127802 |
| 1700000 | 0.133683 |
| 1800000 | 0.142920 |
| 1900000 | 0.157752 |
Luego podríamos interpolar una función a partir de esos puntos, así obtendríamos la función f(x) = tiempo aproximado que demora nuestro programa cuando n = x
Sin embargo, hacer todo lo anterior para cada idea que se nos ocurra sería muy trabajoso, por eso se busca una manera teórica de obtener una buena cota superior de f(x).
Operaciones básicas
Definamos ciertas operaciones como básicas o fundamentales. Asumiremos que el tiempo que demoran en ejecutarse cualquiera de ellas es el mismo. Estas operaciones son:
- Creación y asignacion de una variable
- Operaciones aritméticas
- Llamada de funciones
Ahora nuestro tarea consistirá en encontrar una función g(x) = cantidad de operaciones básicas que realiza nuestro programa para n = x
Así, considerando que nuestra computadora puede realizar aproximadamente \(T = 10^8\) operaciones básicas por segundo, podemos decir que
\[f(x) \approx \frac{g(x)}{T}\]
Sin embargo, usualmente g(x) tendrá la forma
\[g(x) = a_n x^m + a_{m - 1} x^{m - 1} \dots a_1 x + a_0\]
Pero solo consideraremos el término de mayor grado y no tendremos en cuenta las constantes, es decir consideraremos que
\[g(x) = x^m\]
Esto significa que \[g(x) \in O(x^m)\]
Pero se suele escribir \[g(x) = O(x^m)\]
Esta parte se explicará con más detalle en la pizarra
Ejemplos
\[g(n) = 5n + 12 = O(n)\]
\[g(n) = 100.1 n ^ 2 + \pi n + 1 = O(n^2)\]
\[g(n) = 100 = O(1)\]
Y como en general queremos quedarnos con el término que más aporte a la función y eliminar constantes, tenemos los siguientes ejemplos:
\[g(n) = n! + n^2 = O(n!)\]
\[g(n) = 2^n + n^5 = O(2^n)\]
\[g(n) = n \log n + n = O(n \log n)\]
\[g(n) = n \sqrt{n} + n^2 = O(n^2)\]
Usos prácticos
| input size | usually valid time complexity |
|---|---|
| \(n \leq 10\) | \(O(n!)\) |
| \(n \leq 20\) | \(O(2^n)\) |
| \(n \leq 500\) | \(O(n^3)\) |
| \(n \leq 5000\) | \(O(n^2)\) |
| \(n \leq 10^6\) | \(O(n) \text{ or } O(n \log n)\) |
| \(n > 10^6\) | \(O(1) \text{ or } O(\log n)\) |
Fuente: Antti Laaksonen.Competitive programmer’s handbook - chapter 2 (lectura recomendada)
Se verán algunos ejemplos más en la pizarra
La STL es una colección de librerías de C++ que podremos usar en los concursos de programación. Esta nos facilitará estructuras comúnes (array, stack, set, priority_queue, map, ...), algoritmos comúnes (sort, next_permutation, binary_search, lower_bound, upper_bound, ...), funciones comúnes (Input-Output (I/O), sqrt, pow, abs, min, max, ...).
Antes de estudiar lo que nos ofrece la STL comencemos entendiendo como funciona un programa sencillo:
#include <bits/stdc++.h>
using namespace std;
int main () {
cout << "Hola mundo" << '\n';
return 0;
}La explicación se dará en la pizarra
Extra: En realidad también puedes practicar competitiva en otros lenguajes.
Ejemplos:
Pero lo recomendable es C++ por su eficiencia y simplicidad.
Tipos de datos enteros
int\([-2^{31}, 2^{31}) \approx [-10^9, 10^9]\)long long\([-2^{63}, 2^{63}) \approx [-10^{18}, 10^{18}]\)
Tipos de datos flotantes
- float
- double
- long double
Operaciones aritméticas
- suma: x + y
- resta: x - y
- producto: x * y
- división: x / y (cuidado si quieres el resultado en
floatpero 'x', 'y' son enteros) - exponenciación: pow(x, y) (te retorna el resultado en
double)
Orden de precedencia
int < long long < float < double < long double
Ejemplos:
int x = 1;
long long y = 8;
auto z = x + y; // long longint x = 1;
float y = 8;
auto z = x + y; // floatOtro tipo de dato muy utilizado es string.
En cplusplus.com encontrarás una referencia de como puedes operar con strings. Las operaciones más comúnes son:
string s;
// lectura
cin >> s; // así también se lee un int, long long, float, ...
// recorrido
for (int i = 0; i < s.size(); i++) {
// s[i]: accede al elemento en la posicion i
cout << s[i] << '\n'; // así también se imprime un int, long long, float, ...
}
s[2] = 'b'; // así se modifica el caracter en una posición
// así podemos imprimir todo el string
cout << s << '\n';
s += 'a'; // así podemos agregar la letra 'a' al final del string s
cout << s.substr(2, 2) << '\n'; // chequear que hace esto
// la comparación es igual que con los otros tipos de datos
if (s == "hola") cout << "ok" << '\n';En cplusplus.com encontrarás una referencia de como puedes operar con vectores. Las operaciones más comúnes son:
vector <int> arr;
// Agregar un elemento al final - O(1)
arr.push_back(123);
arr.push_back(987);
arr.push_back(343);
arr.push_back(134);
arr.push_back(345);
// Quitar un elemento del final - O(1)
arr.pop_back();
// Agregar un elemento en la posición `i` - O(n)
int i = 2;
arr.insert(begin(arr) + i, 234);
// Eliminar un elemento de la posición `i` - O(n)
i = 1;
arr.erase(begin(arr) + i);
// Copiar el vector - O(n)
vector <int> arrCopy = arr;
// Para iterar el arr podemos hacerlo así:
for (int arr_i: arr) ;
// O también asi
// arr.size() nos retorna la cantidad de elementos - O(1)
for (int i = 0; i < arr.size(); i++) ;
// Si queremos eliminar todos los elementos - O(n)
arr.clear();En resumen, los métodos más frecuentes para vectores son:
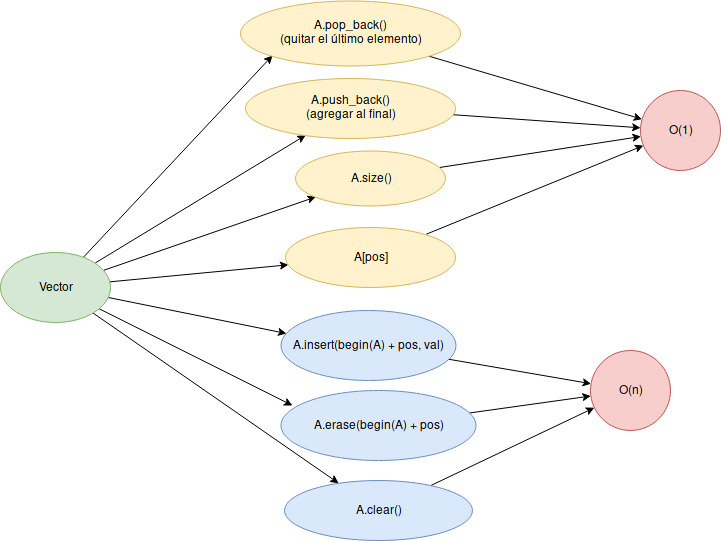
Y un deque nos permite lo mismo que un vector, pero tienes 2 métodos extras
push_front: Inserta un elemento al inicio en O(1)
pop_front: Eliminae el primer elemento en O(1)
Investigar que hacen las siguientes funciones:
Pregunta: ¿Y cómo se declararía una matriz?
En cplusplus.com encontrarás una referencia de como puedes operar con set. Las operaciones más comúnes son:
set <int> S;
// Insertar un elemento - O(log n)
S.insert(3);
S.insert(4);
S.insert(-100);
S.insert(-345);
// Comprobemos que los elementos son guardados en orden ascendente
for (auto x: S) {
cout << x << endl;
}
// Ver si un elemento pertenece al Set - O(log n)
if (S.count(4) > 0) {
cout << "4 esta en el Set\n";
}
// Tambien podemos usar find para esto
if (S.find(4) != end(S)) {
cout << "4 esta en el Set" << endl;
}
// Eliminar un elemento - O(log n)
S.erase(4);
// Tambien podemos eliminar así
S.erase(S.find(-100));
// Si previamente guardamos
// auto it = S.find(val) - O(log n)
// Luego
// S.erase(it) - O(1)En resumen, los métodos más frecuentes para sets son:
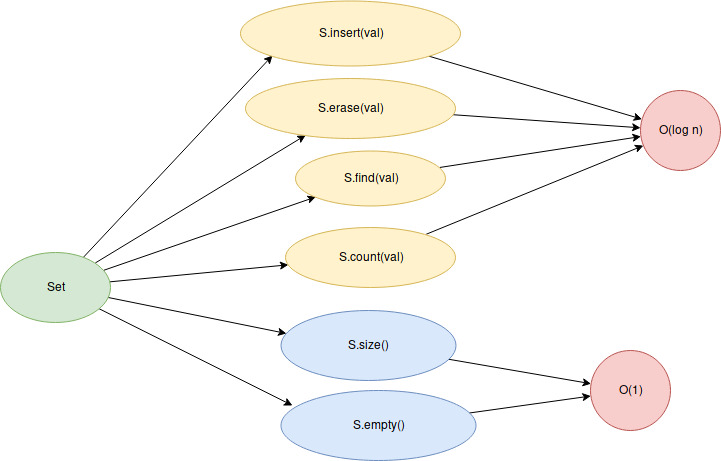
Leer sobre multisets
En cplusplus.com encontrarás una referencia de como puedes operar con maps.
Las complejidad de sus operaciones es la misma que la de un set.
Se recomienda leer Antti Laaksonen.Competitive programmer’s handbook - chapter 1 y 4. La sección 1.4 te ayudará a entender las prácticas que comúnmente encontrarás en competitiva (que eventualmente terminarás usando) y en el capítulo 4 podrás ver más ejemplos de como usar vector, set, map y algunas cosas más.
También te puede interesar:
El contest lo puedes encontrar aquí.
A: Theatre Square
Problem A: Theatre Square
Básicamente necesitamos encontrar \(x * y\) donde
\(x = min\{x \mid x * a \geq n\}\)
\(y = min\{y \mid y * a \geq m\}\)
Entonces, \[x = \lceil \frac{n}{a} \rceil \land y = \lceil \frac{m}{a} \rceil \] Y tenemos la siguiente propiedad: \[\lceil a / b \rceil = \lfloor (a + b - 1) / b \rfloor\] El siguiente código usa esta idea.
Code
#include <bits/stdc++.h>
using namespace std;
int main () {
long long n, m, a;
cin >> n >> m >> a;
long long x = (n + a - 1) / a;
long long y = (m + a - 1) / a;
cout << x * y << '\n';
return (0);
}¿Qué pasa si usamos int en lugar de long long? (intenta \(n = m = 10^9, a = 1\))
B: Shuffle Hashing
Problema B: Shuffle Hashing
Si se puede formar h a partir de p entonces existen \(s_1, s_2, q \mid h = s_1 + q + s_2\)
De manera que \(h[n:n + m] = q\) donde n es el tamaño de \(s_1\) y m el tamaño de p.
Entonces \(sort(h[n:n + m]) = sort(p)\)
Entonces probaremos si se cumple eso para algun tamaño de \(n\).
Code
#include <bits/stdc++.h>
#define all(A) begin(A), end(A)
#define rall(A) rbegin(A), rend(A)
#define sz(A) int(A.size())
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long ll;
typedef pair <int, int> pii;
int main () {
ios::sync_with_stdio(false); cin.tie(0);
int tc;
cin >> tc;
while (tc--) {
string p, h;
cin >> p >> h;
bool ok = false;
sort(all(p));
for (int i = 0; i < sz(h); i++) {
string x = h.substr(i, sz(p));
sort(all(x));
if (x == p) ok = true;
}
if (ok) cout << "YES\n";
else cout << "NO\n";
}
return (0);
}C: Chat Server
Problema C: Chat Server's Outgoing Traffic
Solo simula lo que te dice el problema.
Code
#include <bits/stdc++.h>
#define all(A) begin(A), end(A)
#define rall(A) rbegin(A), rend(A)
#define sz(A) int(A.size())
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long ll;
typedef pair <int, int> pii;
int main () {
ios::sync_with_stdio(false); cin.tie(0);
int ans = 0;
int cur = 0;
string s;
while (getline(cin, s)) {
if (s[0] == '+') {
cur++;
} else if (s[0] == '-') {
cur--;
} else {
int pos = 0;
while (s[pos] != ':') pos++;
ans += (sz(s) - pos - 1) * cur;
}
}
cout << ans << '\n';
return (0);
}D: Counting-out Rhyme
Problema D: Counting-out Rhyme
Los constrains son pequeños, podemos simplemente simular lo que nos dice el problema.
Code
#include <bits/stdc++.h>
#define all(A) begin(A), end(A)
#define rall(A) rbegin(A), rend(A)
#define sz(A) int(A.size())
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long ll;
typedef pair <int, int> pii;
int main () {
ios::sync_with_stdio(false); cin.tie(0);
int n, k;
cin >> n >> k;
vector <int> arr(n);
iota(all(arr), 1);
int cur = 0;
for (int i = 0; i < k; i++) {
int a;
cin >> a;
a %= sz(arr);
while (a--) cur = (cur + 1) % sz(arr);
cout << arr[cur] << ' ';
arr.erase(begin(arr) + cur);
cur %= sz(arr);
}
return (0);
}