Conjunto potencia

El conjunto potencia de un conjunto es el conjunto de todos sus subconjuntos. Por ejemplo:

\[A = \{1, 2, 3\}\] \[P(A) = \{\emptyset, \{1\}, \{2\}, \{3\}, \{1, 2\}, \{2, 3\}, \{1, 3\}, \{1, 2, 3\} \}\]

Donde \(P(A)\) representa el conjunto potencia de \(A\). Además, tenemos que \(|P(A)| = 2^{|A|}\).

Extra: En algunos libros, \(P(A)\) es escrito como \(2^{A}\) (e.g Motousek - Invitation to Discrete Mathematics).

Podemos generar el conjunto potencia de un conjunto usando recursión, pero antes de eso recordemos las distintas formas de pasar argumentos a una función en C++.

#include <bits/stdc++.h>
     
using namespace std;
     
// Pasamos una referencia a 'arr' en O(1)
// PUEDES leer de 'arr', pero NO PUEDES modificarlo
void f1 (const vector <int>& arr) {

}

// Pasamos una referencia a 'arr' en O(1)
// PUEDES leer de 'arr' y PUEDES modificarlo
void f2 (vector <int>& arr) {
}
     
// Pasamos una copia de 'arr' en O(n)
// PUEDES leer de 'arr' y PUEDES modificarlo
// PERO estas modificando la copia de 'arr', no el 'arr' de 'main'
void f3 (vector <int> arr) {
     
}
     
int main () {
  int n = 10000;
  vector <int> arr(n);
  for (int i = 0; i < n; i++) {
    arr[i] = i;
  }
  f1(arr);
  f2(arr);
  f3(arr);
  return (0);
}

Ahora, regresando al problema de generar el conjunto potencia de un conjunto. Primero, veamos un ejemplo pequeño. Si queremos generar el conjunto potencia de \(A = \{1, 2, 3\}\), podemos escribir una función que siga estos estados:

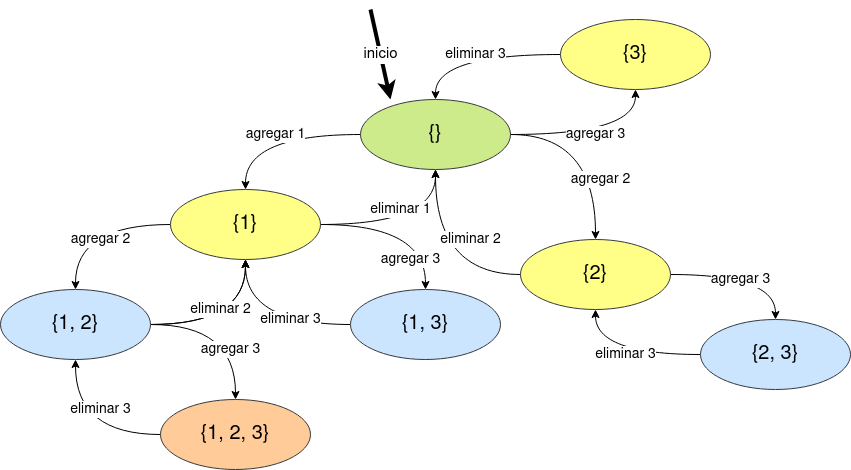
Esto es, si estamos en el estado \((a_1, a_2, \dots a_x) \mid a_1 < a_2 < \dots < a_x\), entonces podemos ir al estado \((a_1, a_2, \dots, a_x, a_y) \mid a_x < a_y \leq n\).

Y podemos implementar esta idea usando recursión así:

#include <bits/stdc++.h>

using namespace std;

void print (const vector <int>& arr) {
  cout << "{";
  bool first = true;
  for (int elem: arr) {
    if (!first) {
      cout << ", ";
    }
    cout << elem;
    first = false;
  }
  cout << "}\n";
}

void backtrack (vector <int>& arr, const int n) {
  print(arr);
  int ax = 0;
  if (!arr.empty()) {
    ax = arr.back();
  }
  for (int ay = ax + 1; ay <= n; ay++) {
    // agrega ay
    arr.push_back(ay);
    backtrack(arr, n);
    // elimina ay
    arr.pop_back();
  }
}

int main () {
  int n = 3;
  vector <int> subset;
  backtrack(subset, n);
}

Pero, en programación competitiva, es común tratar de tener pocos argumentos en nuestras funciones, por ello se suele hacer constante uso de variables globales. Por ejemplo, la anterior solución se puede modificar de esta manera (¿por qué?):

#include <bits/stdc++.h>

using namespace std;

void print (const vector <int>& arr) {
  cout << "{";
  bool first = true;
  for (int elem: arr) {
    if (!first) {
      cout << ", ";
    }
    cout << elem;
    first = false;
  }
  cout << "}\n";
}

// variables globales
vector <int> subset;
int n;

void backtrack () {
  print(subset);
  int ax = 0;
  if (!subset.empty()) {
    ax = subset.back();
  }
  for (int ay = ax + 1; ay <= n; ay++) {
    // add ay
    subset.push_back(ay);
    backtrack();
    // delete ay
    subset.pop_back();
  }
}

int main () {
  n = 3;
  backtrack();
}

Así, hemos implementado un programa que encuentra el conjunto potencia del conjunto \(\{1, 2, 3, \dots, n\}\) en \(O(n 2 ^ n)\). Las soluciones presentadas han usado una técnica conocida como backtracking. En general, una solución backtracking tiene esta forma:

sea state una variable global

T backtrack (algunos parámetros):
  if (state es un estado terminal):
    Realiza algo con 'state' y retorna algo
  
  for (state' alcanzable desde state):
    # Realiza algo
    previous = state
    state = state'
    backtrack(algunos parámetros')
    # Revierte cambios
    state = previous

Un estado terminal es un estado en donde ya no podemos ir a otros estados (o donde no es conveniente seguir buscando).

Veamos como podemos usar esta técnica en este problema.

Podemos tomar los elementos de indices \(\{i_1, i_2, \dots, i_k\} \subseteq \{1, 2, 3, \dots, n\}\). Así, podemos buscar la solución en el conjunto potencia de \(\{1, 2, 3, \dots, n\}\) usando backtracking.

#include <bits/stdc++.h>
     
#define all(A) begin(A), end(A)
#define rall(A) rbegin(A), rend(A)
#define sz(A) int(A.size())
#define pb push_back
#define mp make_pair
     
using namespace std;
     
typedef long long ll;
typedef pair <int, int> pii;
typedef vector <int> vi;
typedef vector <ll> vll;

int n;
vi v, c;

int backtrack (int pos, int x, int y) {
  if (pos == n) return x - y;
  return max(backtrack(pos + 1, x + v[pos], y + c[pos]), backtrack(pos + 1, x, y));
}

int main () {
  ios::sync_with_stdio(false); cin.tie(0);
  cin >> n;
  v.resize(n);
  c.resize(n);
  for (int& elem: v) cin >> elem;
  for (int& elem: c) cin >> elem;
  cout << backtrack(0, 0, 0) << '\n';
  return (0);
}

El problema de la mochila 0-1

Problema: Tienes una mochila de capaidad \(W\) (i.e puedes poner como máximo \(W\) kg en la mochila). Además, tienes \(n\) accesorios. Cada accesorio es descrito como un par \((val_i, w_i)\), donde \(val_i\) es el costo de ese accesorio y \(w_i\) su peso. Encuentra el máximo valor que puedes guardar en la mochila usando el menor peso posible.

\[1 \leq n \leq 16\]

Solución:

Cada accesorio puedes ser tomado o no, entonces podemos buscar por todas las posibilidades (conjunto potencia) usando backtracking.

#include <bits/stdc++.h>

using namespace std;

int n;
int W;
vector <int> val;
vector <int> w;
vector <int> take;
int max_sum_val = 0;
int min_sum_w = 0;
vector <int> ans_items_taken;

void backtrack (int last_taken, int sum_val, int sum_w) {
  if (sum_w <= W and (sum_val > max_sum_val or
      (sum_val == max_sum_val and sum_w < min_sum_w))) {
    max_sum_val = sum_val;
    min_sum_w = sum_w;
    ans_items_taken = take;
  }
  for (int i = last_taken + 1; i < n; i++) {
    take.push_back(i);
    backtrack(i, sum_val + val[i], sum_w + w[i]);
    take.pop_back();
  }
}

int main () {
  n = 3;
  W = 10;
  // item 1
  val.push_back(10);
  w.push_back(10);
  // item 2
  val.push_back(1);
  w.push_back(8);
  // item 3
  val.push_back(13);
  w.push_back(2);
  backtrack(-1, 0, 0);

  cout << "Take items";
  for (int item: ans_items_taken) {
    cout << ' ' << item + 1;
  }
  cout << '\n';
  return (0);
}

Permutaciones

El problema de generar todas las permutaciones puede ser fácilmente resuelto en \(O(n n!)\) usando backtracking.

#include <bits/stdc++.h>

using namespace std;

int n;
vector <bool> used;
vector <int> permutation;

void print (const vector <int>& p) {
  for (int elem: p) {
    cout << elem << ' ';
  }
  cout << '\n';
}

void backtrack () {
  if (permutation.size() == n) {
    print(permutation);
    return;
  }
  for (int p_i = 1; p_i <= n; p_i++) {
    if (!used[p_i]) {
      used[p_i] = true;
      permutation.push_back(p_i);
      backtrack();
      used[p_i] = false;
      permutation.pop_back();
    }
  }
}

int main () {
  n = 3;
  used.resize(n + 1, false);
  backtrack();
  return (0);
}

Aqui estamos siguiendo estos estados:

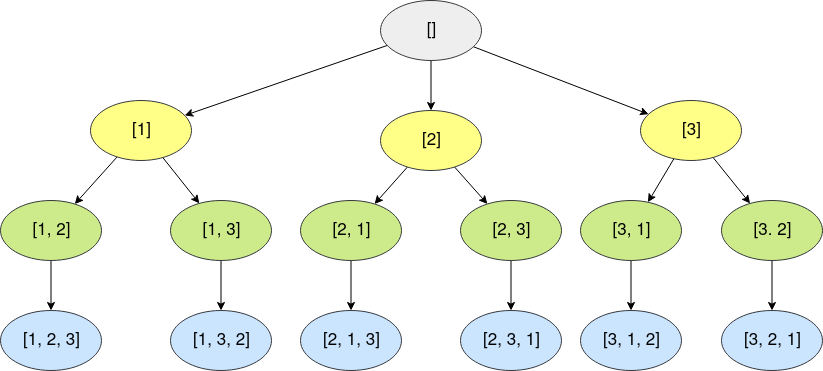
Esta imagen representa lo que se conoce como el árbol de recursión, ese nos muestra como la función hace las transiciones.

Además, notamos que no necesitamos hacer algo como esto:

.
.
.
  for (int p_i = 1; p_i <= n; p_i++) {
    if (!used[p_i]) {
      vector <bool> used_previous = used;
      vector <int> permutation_previous = permutation;
      used[p_i] = true;
      permutation.push_back(p_i);
      backtrack();
      used = used_previous;
      permutation = permutation_previous;
    }
  }
.
.
.

Porque esto sería más pesado que la primera solucion y porque sabemos que:

De estas observaciones notamos que cuando en tu recursión estás en estado y vas a state', entonces después de recorrer el árbol de recursion de state' debes tener las variables en el mismo estado previo a comenzar la recursión por el árbol de state'. Entender estas observaciones es clave para entender backtracking.

Sudoku

Con backtracking es fácil generar todas los posibles movimientos de un juego y escoger el mejor movimiento.

Problema:

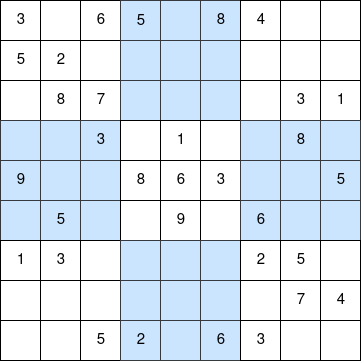
Completa el sudoku de arriba de tal manera que cada número del 1 al 9 es encontrado solo una vez en cada fila, columna y cuadrante.

Solución: Podemos buscar todas las posibilidades usando backtracking.

#include <bits/stdc++.h>

using namespace std;

vector <vector <int>> sudoku;
vector <vector <int>> sudoku_solved;
vector <vector <pair <int, int>>> quadrant;
int n;
int N;
bool found;

bool validInRow (int r, int d) {
  for (int c = 0; c < N; c++) {
    if (sudoku[r][c] == d) return false;
  }
  return true;
}

bool validInCol (int c, int d) {
  for (int r = 0; r < N; r++) {
    if (sudoku[r][c] == d) return false;
  }
  return true;
}

bool validInQuadrant (int q, int d) {
  for (pair <int, int> pos: quadrant[q]) {
    int r = pos.first;
    int c = pos.second;
    if (sudoku[r][c] == d) return false;
  }
  return true;
}

// corre esta funcion for cada 0 <= r < N and 0 <= c < N
// y entederás que es lo que hace
int getQuadrant (int r, int c) {
  return (r / n) * n + (c / n);
}

void backtrack (int r, int c) {
  if (r == N) {
    found = true;
    sudoku_solved = sudoku;
    return;
  }
  if (found) {
    return;
  }
  int nc = (c + 1 == N) ? 0 : c + 1; // new column
  int nr = (c + 1 == N) ? r + 1 : r; // new row
  if (sudoku[r][c] != 0) {
    backtrack(nr, nc);
    return;
  } 
  for (int d = 1; d <= 9; d++) {
    int quadrant = getQuadrant(r, c);
    if (validInRow(r, d) and
        validInCol(c, d) and
        validInQuadrant(getQuadrant(r, c), d)) {
      sudoku[r][c] = d;
      backtrack(nr, nc);
      sudoku[r][c] = 0;
    }
  }
}

void precomputation () {
  found = false;
  N = sudoku.size();
  n = 1;
  while ((n + 1) * (n + 1) <= N) n++;
  // n = sqrt(N)
  quadrant.resize(N);
  for (int r = 0; r < N; r++) {
    for (int c = 0; c < N; c++) {
      quadrant[getQuadrant(r, c)].push_back({r, c});
    }
  }
}

void print (const vector <vector <int>>& sudoku) {
  for (auto row: sudoku) {
    for (int elem: row) {
      cout << elem << ' ';
    }
    cout << '\n';
  }
}

int main () {
  sudoku = {
            {3, 0, 6, 5, 0, 8, 4, 0, 0},  
            {5, 2, 0, 0, 0, 0, 0, 0, 0},  
            {0, 8, 7, 0, 0, 0, 0, 3, 1},  
            {0, 0, 3, 0, 1, 0, 0, 8, 0},  
            {9, 0, 0, 8, 6, 3, 0, 0, 5},  
            {0, 5, 0, 0, 9, 0, 6, 0, 0},  
            {1, 3, 0, 0, 0, 0, 2, 5, 0},  
            {0, 0, 0, 0, 0, 0, 0, 7, 4},  
            {0, 0, 5, 2, 0, 6, 3, 0, 0}
           };
  precomputation();
  backtrack(0, 0);
  print(sudoku_solved);
  return (0);
}

Con este código podemos obtener esta solución:

El problema de las N-reinas

Problema:

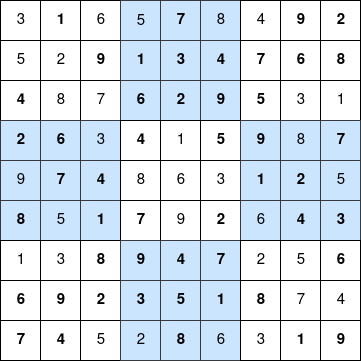
Dado un tablero de ajedrez de \(N \times N\) celdas, debes colocar \(N\) reinas en el tablero de tal manera que no se ataquen.

\[1 \leq N \leq 10\]

Recuerda: Una reina puede atacar en toda una fila, columna o diagonal.

Solución: Podemos intentar poner \(N\) reinas en las \(N \times N\) celdas. De esta manera tendríamos \(\binom{N \times N}{N}\) estados que verificar. Pero para \(N = 8\) tenemos \(\binom{N \times N}{N} \approx 8B\) estados, entonces necesitamos un mejor enfoque.

Sabemos que cada reina debe estar en distintas columnas (sino ellas se estarían atacando entre sí). Entonces podemos generar estas \(N^N\) configuraciones y revisar si las condiciones se cumplen. Pero para este problema este enfoque no es suficiente.

Analizando un poco nos damos cuenta que cada reina debe estar en una fila y columna distinta. Así, las filas de las posiciones de las reinas en una configuración válida forman son una permutación de \(\{ 1, 2, \dots, n }\), lo mismo se cumple con las columnas. De este modo, tenemos \(N!\) posibles configuraciones que revisar y podemos implementar este enfoque con backtracking.

#include <bits/stdc++.h>

using namespace std;

int n;
vector <pair <int, int>> queen;
vector <pair <int, int>> solution;

bool valid (int r, int c) {
  for (auto pp: queen) {
    // if same row or same column or same diagonal
    if ((pp.first == r) or
        (pp.second == c) or
        (abs(r - pp.first) == abs(c - pp.second))) {
      return false;
    }
  }
  return true;
}

void backtrack (int r) {
  if (r == n) {
    solution = queen;
    return;
  }
  if (!solution.empty()) {
    return;
  }
  for (int c = 0; c < n; c++) {
    if (valid(r, c)) {
      queen.push_back({r, c});
      backtrack(r + 1);
      queen.pop_back();
    }
  }
}

int main () {
  cin >> n;
  backtrack(0);
  if (solution.empty()) {
    cout << "NO\n";
    return (0);
  }
  vector <vector <int>> board(n, vector <int> (n, 0));
  for (auto pp: solution) {
    board[pp.first][pp.second] = 1;
  }
  cout << "YES\n";
  for (int r = 0; r < n; r++) {
    for (int c = 0; c < n; c++) {
      cout << board[r][c] << " \n"[c == n - 1];
    }
  }
  return (0);
}

Para \(N = 4\) el árbol de recursión de nuestra solución luce así:

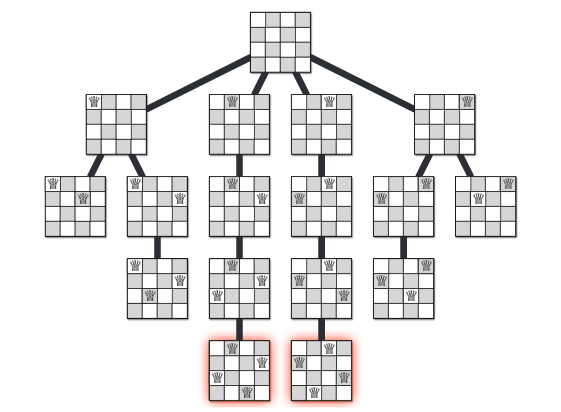
Imagen tomada de Jeff Erickson - Algorithms - Chapter 2: Backtracking.

La complejidad de la anterior solución viene de la equación:

\[T_n = n \cdot T_{n - 1} + O(n)\] \[\to T_n = O(n!)\]

Así, nuestra solución tiene complejidad \(O(n!)\).

Lecturas recomendadas:

También te podría interesar ver este documental de AlphaGo. Aquí está el trailler.

Contest

El contest lo puedes encontrar aquí.

CD

Cada elemento puede o no ser tomado, entonces podemos implementar una solución backtracking; además, de esta manera podemos mantener el orden inicial de los elementos.

#include <bits/stdc++.h>
     
using namespace std;
 
int main () {
  int n;
  while (cin >> n) {
    int m;
    cin >> m;
    vector <int> arr(m);
    for (int& elem: arr) cin >> elem;
    vector <int> take;
    vector <int> ans;
    int sum = 0;
    int best_sum = 0;

    function <void(int)> backtrack = [&] (int pos) -> void {
      if (sum > best_sum or (sum == best_sum and ans.size() < take.size())) {
        best_sum = sum;
        ans = take;
      }
      if (pos == m) return;
      // do not take it
      backtrack(pos + 1);
      if (sum + arr[pos] > n) return;
      // take it
      take.push_back(arr[pos]);
      sum += arr[pos];
      backtrack(pos + 1);
      take.pop_back();
      sum -= arr[pos];
    };

    backtrack(0);
    for (int elem: ans) cout << elem << ' ';
    cout << "sum:" << best_sum << '\n';
  }
  return (0);
}

Hanoi Tower Troubles Again!

Hay un enfoque greedy: pon el balón en la primera pila donde puedas ponerlo.

#include <bits/stdc++.h>

using namespace std;

int main () {
  const int N = 1e5;
  vector <bool> is_sq(N, false);
  for (int i = 0; i * i < N; i++) is_sq[i * i] = true;
  int tc;
  cin >> tc;
  while (tc--) {
    int n;
    cin >> n;
    vector <vector <int>> pile(n);
    int ans = 0;
    int cur = 0;

    function <void(int)> rec = [&] (int num) -> void {
      ans = max(ans, cur);
      for (int i = 0; i < n; i++) {
        if (pile[i].empty() or is_sq[pile[i].back() + num]) {
          cur += 1;
          pile[i].push_back(num);
          rec(num + 1);
          break;
        }
      }
    };

    rec(1);
    cout << ans << '\n';
  }
  return (0);
}

Marcus

Identifica el punto inicial y luego busca en la matriz usando backtracking.

#include <bits/stdc++.h>

using namespace std;

int main () {
  const vector <int> dr = {-1, 0, 0};
  const vector <int> dc = {0, -1, 1};
  const vector <string> option = {"forth", "left", "right"};
  const string word = "IEHOVA#";
  int tc;
  cin >> tc;
  while (tc--) {
    int n, m;
    cin >> n >> m;
    vector <string> ans;
    vector <string> take;
    vector <string> grid(n);
    for (int i = 0; i < n; i++) cin >> grid[i];

    function <void(int,int)> backtrack = [&] (int r, int c) -> void {
      if (take.size() == 7) {
        ans = take;
        return;
      }
      for (int d = 0; d < 3; d++) {
        if (!ans.empty()) return;
        int nr = r + dr[d];
        int nc = c + dc[d];
        if (not (0 <= min(nr, nc) and nr < n and nc < m)) continue;
        if (grid[nr][nc] != word[take.size()]) continue;
        take.push_back(option[d]);
        backtrack(nr, nc);
        take.pop_back();
      }
    };

    for (int r = 0; r < n; r++) {
      for (int c = 0; c < m; c++) {
        if (grid[r][c] == '@') {
          backtrack(r, c);
        }
      }
    }
    for (int i = 0; i < 7; i++) {
      cout << ans[i] << " \n"[i == 6];
    }
  }
  return (0);
}

Back to the 8-Queens

Solo hay 92 configuraciones válidas, puedes generarlas con backtracking y luego solo hacer una busqueda lineal por cada test.

#include <bits/stdc++.h>

using namespace std;

const int N = 8;
vector <pair <int, int>> queen;
vector <vector <pair <int, int>>> solution;

bool valid (int r, int c) {
  for (auto pp: queen) {
    // if same row or same column or same diagonal
    if ((pp.first == r) or
        (pp.second == c) or
        (abs(r - pp.first) == abs(c - pp.second))) {
      return false;
    }
  }
  return true;
}

void backtrack (int c) {
  if (c == N + 1) {
    solution.push_back(queen);
    return;
  }
  for (int r = 1; r <= N; r++) {
    if (valid(r, c)) {
      queen.push_back({r, c});
      backtrack(c + 1);
      queen.pop_back();
    }
  }
}

int main () {
  backtrack(1);
  vector <int> row(N);
  int tc = 0;
  while (cin >> row[0]) {
    for (int i = 1; i < N; i++) cin >> row[i];
    int ans = INT_MAX;
    for (auto sol: solution) {
      int need = 0;
      for (int i = 0; i < N; i++) {
        need += (row[i] != sol[i].first);
      }
      ans = min(ans, need);
    }
    cout << "Case " << ++tc << ": " << ans << '\n';
  }
  return (0);
}

Boggle Blitz

Solo implementa una solución backtracking para hacer una búsqueda completa.

#include <bits/stdc++.h>

using namespace std;

int main () {
  int tc;
  cin >> tc;
  for (int t = 0; t < tc; t++) {
    if (t) cout << '\n';
    int n;
    cin >> n;
    vector <string> grid(n);
    for (int i = 0; i < n; i++) cin >> grid[i];
    vector <string> ans;
    string word = "";

    function <void(int,int,char)> backtrack = [&] (int r, int c, char last) -> void {
      if (3 <= word.size()) {
        ans.push_back(word);
      }
      for (int dr = -1; dr <= 1; dr++) {
        for (int dc = -1; dc <= 1; dc++) {
          if (dr == 0 and dc == 0) continue;
          int nr = r + dr;
          int nc = c + dc;
          if (not (0 <= min(nr, nc) and max(nr, nc) < n)) continue;
          if (grid[nr][nc] <= last) continue;
          word += grid[nr][nc];
          backtrack(nr, nc, grid[nr][nc]);
          word.pop_back();
        }
      }
    };

    for (int r = 0; r < n; r++) {
      for (int c = 0; c < n; c++) {
        word += grid[r][c];
        backtrack(r, c, grid[r][c]);
        word.pop_back();
      }
    }
    sort(begin(ans), end(ans), [&] (const string& x, const string& y) {
      if (x.size() != y.size()) return x.size() < y.size();
      return x < y;  
    });
    // delete duplicates
    ans.erase(unique(begin(ans), end(ans)), end(ans));
    for (auto& word: ans) cout << word << '\n';
  }
  return (0);
}