Clase 05: Fuerza Bruta I
Leonidas
21-01-2020
Nota: Algunos términos se dejarán en Inglés por simplicidad en esta y siguientes clases
Un paradigma es una manera de resolver problemas. En competitiva hay 4 paradigmas de problem solving fundamentales:
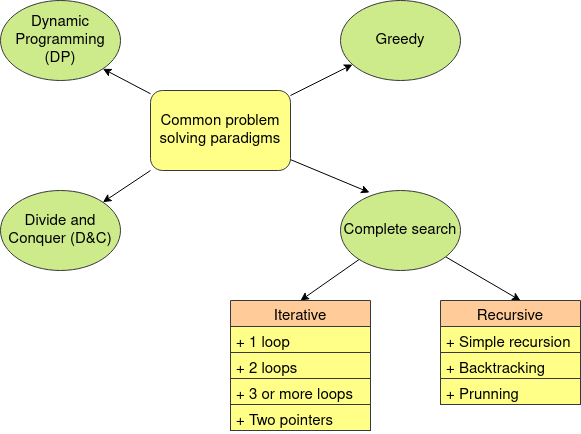
Búsqueda completa es un método general que puede ser usado para resolver casi cualquier problema computacional. Básicamente se trata de generar todas las posibles soluciones de un problema para hacer algo con estas soluciones (contar la cantidad de elementos, encontrar una solución en particular, etc).
Soluciones de búsqueda completa pueden ser encontradas de dos maneras: iterativas o recursivas. Cuando es iterativo lo puedes encontrar como un solo loop, dos loops, tres o más loops, usando two pointers, etc. Cuando es recursivo lo puedes encontrar como una función recursiva simple, como una función recursiva que busca distintos estados mediante trial and error (backtracking), puede tener prunning para no visitar todos los estados, etc.
Cuando resuelvas un problema de búsqueda completa usarás alguna combinación de estas estructuras. Sin embargo, cada problema es distinto y deberá atacarse de manera distinta. No existe una método mágico que funcione para todos los problemas de búsqueda completa, por eso en clases se irá mostrando técnicas conocidas para atacar una gran variedad de problemas. El dominar estas técnicas te ayudará a resolver cada vez una mayor cantidad de problemas y cada vez más dificiles.
Cuando un problema de búsqueda completa se resuelva de manera iterativa diremos que tenemos una solución fuerza bruta. Comenzaremos estudiando este paradigma mostrando distintas técnicas para atacar problemas de fuerza bruta.
Comencemos resolviendo un problema simple.
Una tripleta pitagótica es una tripleta \((x, y, z)\) que satisface la equación \(x^2 + y^2 = z^2\).
Problem: Recibirás un entero \(n\). Encuentra la cantidad de tripletas pitagóricas tal que \(1 \leq x, y, z \leq n\).
\[1 \leq n \leq 10^3\]
Primera solución
Podemos fijar \(x, y, z\) usando tres \(fors\) y verificar la ecuación en \(O(n^3)\).
int solution1 (int n) {
int cnt = 0;
for (int x = 1; x <= n; x++) {
for (int y = 1; y <= n; y++) {
for (int z = 1; z <= n; z++) {
if (x * x + y * y == z * z) {
cnt++;
}
}
}
}
return cnt;
}Segunda solución
Podemos fijar \(x, y\) y determinar si \(\exists \, 1 \leq z \leq n\) que satisface la equación en \(O(n^2).\)
int solution2 (int n) {
vector <bool> is_sq(n * n + 1, false);
for (int z = 1; z <= n; z++) {
is_sq[z * z] = true;
}
int cnt = 0;
for (int x = 1; x <= n; x++) {
for (int y = 1; y <= n; y++) {
if (x * x + y * y <= n * n and is_sq[x * x + y * y]) {
cnt++;
}
}
}
return cnt;
}Tercera solución
Si \((x, y, z)\) es una tripleta pitagórica, entonces \((kx, ky, kz), k \in \mathbb{N}\) también es una tripleta pitagórica.
Entonces, si encontramos \((x, y, z) \mid gcd(x, y, z) = 1\), la cantidad de tripletas \((kx, ky, kz) : 1 \leq kx, ky, kz \leq n\) es \(\min(\lfloor n / x \rfloor, \lfloor n / y \rfloor, \lfloor n / z \rfloor)\).
Además, si \((x, y, z)\) es una tripleta pitagórica y \(gcd(x, y, z) = 1\), entonces \((x, y, z)\) es llamada una tripleta pitagórica primitiva.
Y existe una propiedad (fórmula de Euclides) que nos dice que toda tripleta pitagórica puede ser representada por un par \((a, b) : 0 < b < a \land gcd(a, b) = 1,\) \(a\) y \(b\) no ambos impares. Esta representación es de la siguiente manera:
\[x = a^2 - b^2\] \[y = 2 * a * b\] \[z = a * a + b * b\]
Entonces podemos generar primitivas \((x, y, z), (y, x, z)\) y contar cuantos de sus múltiplos cumplen la condición en \(O(n \log n)\).
int solution3 (int n) {
int cnt = 0;
for (int a = 1; a * a < n; a++) {
for (int b = 1; b < a; b++) {
if (__gcd(a, b) != 1) continue;
if (a % 2 and b % 2) continue;
int x = a * a - b * b;
int y = 2 * a * b;
int z = a * a + b * b;
int add = min({n / x, n / y, n / z});
cnt += 2 * add;
}
}
return cnt;
}Como hemos visto, un problema se puede resolver de distintas formas. Eso es algo interesante, especialmente de los problemas de búsqueda completa, pues con el conocimiento de algunas técnicas y algo de creatidad se pueden crear soluciones interesantes. Ahora, discutiremos algunas técnicas conocidas para atacar problemas de fuerza bruta:
- Fijando variables
- Simulación
- Weak constraints
- Análisis por casos
Y también describiremos brevemente de que trata prefix sums
Hay una clase de problemas donde tienes algunas equaciones en \(m\) variables. En esas ocaciones, una primera buena idea es intentar una solución fuerza bruta. Para ello se encuentra el rango de valores que puede tomar cada variable, se hace un loop for cada una de ellas, se comprueba si las ecuaciones se satisfacen y se va almacenando las m-tuplas que satisfacen las condiciones. También, cuando estamos haciendo un for sobre una variable, estamos fijando su valor, asi dentro de cada for su valor se vuelve una constante, es decir, estamos reduciendo el número de variables. Por eso, usualmente \(m - 1\) for serán suficientes, pues la última variable suele ser fácil de calcular cuando las demás ya son constantes.
Por ejemplo, intentemos este problema.
Problemia: Recibirás \(n, a, b, c\) enteros. Debes encontrar
\[|\{(x, y, z) \mid 0 \leq x \leq a \land 0 \leq y \leq b \land 0 \leq z \leq c \land \frac{x}{2} + y + 2 z = n \}|\]
\[1 \leq n \leq 10^4\] \[0 \leq a, b, c \leq 5000\]
Podemos identificar que las variables del problema son \(x, y, z\) y que si fijamos dos de estas variables podemos obtener la tercera de la equación, entonces una solución fuerza bruta con 2 for puede resolver el problema. Ahora, para determinar que variables fijar, siempre prefiere trabajar con enteros (se entenderá mejor esto en próximas clases), así fijaremos \(y, z\) en \(O(b * c)\).
Code
#include <bits/stdc++.h>
#define all(A) begin(A), end(A)
#define rall(A) rbegin(A), rend(A)
#define sz(A) int(A.size())
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long ll;
typedef pair <int, int> pii;
typedef vector <int> vi;
typedef vector <ll> vll;
int main () {
ios::sync_with_stdio(false); cin.tie(0);
int n, a, b, c;
cin >> n >> a >> b >> c;
int ans = 0;
for (int z = 0; z <= c; z++) {
for (int y = 0; y <= b; y++) {
int left = n - z * 2 - y;
if (left < 0) continue;
int x = left * 2;
if (x <= a) ans++;
}
}
cout << ans << '\n';
return (0);
}Puedes practicar con estos problemas:
- Cut Ribbon
- Economy Game
- Berry Jam
- Hot Bath (Challenge)
En esta clase de problema se suele describir un patrón, fórmula de recurencia or situación que es relativamente sencillo de computar. La clave para estos problemas suele ser darse cuenta como generar tu espacio de búsqueda y saber implementar tus ideas.
Por ejemplo, comencemos con este problema
Problem: Un humble number es un número cuyos únicos factores primos son \(2, 3, 5, 7\). Recibirás un número \(n\) y deberás imprimir el \(n-th\) humble number.
\[1 \leq n \leq 5842\]
Necesitamos calcular \(S = \{2^i \cdot 3 ^j \cdot 5^k \cdot 7 ^l, \quad 0 \leq i, j, k, l \}\). Digamos que el máximo valores que computamos es \(L\), entonces \(i, j, k, l = O(\log L)\).
Así, si fijamos \(L\) podemos obtener los elementos de \(S\) que son menores a \(L\) en \(O((\log^4 L))\). Así, podemos probar distintos valores de \(L\) hasta que obtengamos más números que el máximo \(n\) que recibimos en nuestra entrada. Ten cuidado con el overflow.
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main () {
const ll L = 1e10;
vector <ll> arr;
for (ll two = 1; two < L; two *= 2) {
for (ll three = 1; three < L; three *= 3) {
for (ll five = 1; five < L; five *= 5) {
for (ll seven = 1; seven < L; seven *= 7) {
if (two >= L / three) break;
ll cur = two * three;
if (cur >= L / five) break;
cur *= five;
if (cur >= L / seven) break;
cur *= seven;
arr.push_back(cur);
}
}
}
}
sort(begin(arr), end(arr));
int n;
while (cin >> n) {
if (n == 0) break;
string pos;
if (n % 10 == 1 and (n / 10) % 10 != 1) pos = "st";
else if (n % 10 == 2 and (n / 10) % 10 != 1) pos = "nd";
else if (n % 10 == 3 and (n / 10) % 10 != 1) pos = "rd";
else pos = "th";
cout << "The " << n << pos << " humble number is " << arr[n - 1] << ".\n";
}
return (0);
}Puedes practicar con estos problemas:
En esta clase de problemas el enunciado usualemente luce dificil, pero una vez que identificas el espacio de búsqueda te daras cuenta que el número de posibles soluciones es pequeño.
For ejemplo, resolvamos este problema.
Problema: Encuentra
\[|\{x \leq n \mid x - f(x) \geq s\}|\]
Donde \(f(x) =\) suma de dígitos de \(x\).
\[1 \leq n, s \leq 10^{18}\]
A primera vista el problema luce dificil, pero tenemos:
\[0 \leq f(x) \leq 9 * 18\] \[\to x - 9 * 18 \leq x - f(x) \leq 9 * 18\]
Encontes, solo necesitamos buscar la respuesta en \([s, s + 9 * 18]\). ¿Qué pasa si un número es mayor que \(s + 9 * 18\)?
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MX_SUM = 9 * 18;
int sumOfDigits (ll num) {
int ret = 0;
while (num) ret += (num % 10), num /= 10;
return ret;
}
int main () {
ll n, s;
cin >> n >> s;
ll ans = 0, k;
for (k = s; k <= min(n, s + MX_SUM); k++) {
if (k - sumOfDigits(k) >= s) ans++;
}
ans += max(0LL, n - k + 1);
cout << ans << endl;
return (0);
}La clave para resolver este tipo de problemas es identificar que el espacio de búsqueda es pequeño debido a alguna propiedad o que una de las variables de la entrada es pequeña y que podemos intentar una solución fuera bruta sobre ella.
Este tipo de problemas suelen parecer complicados, pero cuando analizar los casos que pueden ocurrir te das cuenta que el problema se reduce a algo mucho más simple.
Por ejemplo, analicemos este problema.
Problema: Te dan un array \(a\) de \(n\) elementos. Imprime dos números \(i, j \mid a_i \not = a_j \land i < j\) tal que cuando intercambiamos \(a_i, a_j\) el array no esta ordenado (de forma ascendente ni descendente) o imprime -1 si tal par de números no existe.
\[1 \leq n \leq 10^5\]
Una primera idea sería fijar \(i, j\) con dos \(for\) y verificar si las condiciones se cumplen. Esta solución es \(O(n^3)\), por eso así obtendriamos un TLE. Necesitamos algo mejor.
Analicemos el problema por casos de acuerdo a la cantidad de elementos distintos que tiene el array.
- Caseo 1: Todos los elementos son iguales
Entonces, la respues es -1.
- Caso 2: Hay más de 2 elementos diferentes.
Puedes tomar 3 elementos distintos cualquiera y encontrarás una respuesta en ellos (¿puedes probarlo?).
- Caso 3: Hay exactamente 2 elementos diferentes.
Fijemos \(x = a_i\) y \(y = a_j\).
- Caso 3.1: \(a_i < a_j\)
Si los intercambiamos el array no puede estar en orden creciente. Si el array no está en orden decreciente, entonces tenemos una respuesta, sino el array tiene la forma:
\[a_1 = y \geq a_2 = y \geq \dots \geq a_i = y \geq \dots \geq a_j = x \geq \dots \geq a_n =x\]
Entonces, si existe una respuesta, esta debe estar en \([i, j)\) o \((i, j]\). Así, solo necesitamos verificar un par de enteros \((i, i - 1) \mid a_i < a_{i+ 1}\).
- Caso 3.2: \(a_i > a_j\)
Si los intercambiamos el array no puede estar en orden decreciente. Si el array no está en orden creciente, entonces tenemos una respuesta, sino el array tiene la forma:
\[a_1 = x \leq a_2 = x \leq \dots \leq a_i = x \leq \dots \leq a_j = y \leq \dots \leq a_n =y\]
Entonces, si existe una respuesta, esta debe estar en \([i, j)\) o \((i, j]\). Así, solo necesitamos verificar un par de enteros \((i, i - 1) \mid a_i > a_{i+ 1}\).
Usando todos estos casos podemos implementar una solución en \(O(n \log n)\).
Code
#include <bits/stdc++.h>
using namespace std;
int main () {
int n;
cin >> n;
set <int> values;
map <int, int> pos;
vector <int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
pos[a[i]] = i;
values.insert(a[i]);
}
if (values.size() == 1) {
cout << -1 << '\n';
return (0);
}
vector <int> a_inc = a;
vector <int> a_dec = a;
sort(begin(a_inc), end(a_inc));
sort(begin(a_dec), end(a_dec));
reverse(begin(a_dec), end(a_dec));
if (values.size() > 2) {
vector <int> arr;
for (auto pp: pos) {
arr.push_back(pp.second);
}
for (int i = 0; i < 3; i++) {
for (int j = i + 1; j < 3; j++) {
int x = arr[i];
int y = arr[j];
swap(a[x], a[y]);
if (a != a_inc and a != a_dec) {
cout << 1 + min(x, y) << ' ' << 1 + max(x, y) << '\n';
return (0);
}
swap(a[x], a[y]);
}
}
}
for (int i = 0; i + 1 < n; i++) {
if (a[i] < a[i + 1]) {
swap(a[i], a[i + 1]);
if (a != a_dec) {
cout << 1 + i << ' ' << 1 + i + 1 << '\n';
return (0);
}
swap(a[i], a[i + 1]);
break;
}
}
for (int i = 0; i + 1 < n; i++) {
if (a[i] > a[i + 1]) {
swap(a[i], a[i + 1]);
if (a != a_inc) {
cout << 1 + i << ' ' << 1 + i + 1 << '\n';
return (0);
}
swap(a[i], a[i + 1]);
break;
}
}
cout << -1 << '\n';
return (0);
}Puedes practicar con estos problemas:
- Shawarma Tent
- Interesting Subarray
- Divide by Three (Challenge)
Prefix sums es una técnica simple, pero poderosa.
Veamosla en este problema.
Problema: Recibirás un array de \(N\) elementos y \(Q\) consultas. Cada consulta es un rango \(l, r\). Por cada consulta imprime the suma de elementos del array en las posiciones \([l, r]\).
Sea \(prefix(x) = a_0 + a_1 + a_2 + \dots + a_x\) y \(prefix(-1) = 0\). Entonces:
\(\displaystyle\sum_{i=l}^{r}a_i = prefix(r) - prefix(l - 1)\).
Entonces, podemos calcular \(prefix\) usando un array en \(O(n)\) y responder cada consulta en \(O(1)\) resolviendo así el problema en \(O(n + q)\).
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
vector <ll> prefix;
ll get (int pos) {
if (pos == -1) return 0;
return prefix[pos];
}
int main () {
cin >> n;
prefix.resize(n);
for (int i = 0; i < n; i++) {
int a;
cin >> a;
prefix[i] = a + get(i - 1);
}
int q;
cin >> q;
while (q--) {
int l, r;
cin >> l >> r;
cout << get(r) - get(l - 1) << '\n';
}
return (0);
}Puedes practicar con estos problemas:
Lecturas recomendadas:
- Notas de fuerza bruta
- PCUNI-2019 Clase 05
- Topcoder - Representation of integers and reals section 1
- Topcoder - Representation of integers and reals section 2
El contest lo puedes encontrar aquí.
A: Simple Equations
Simple Equations
\[0 \leq x^2 \quad \forall x \in \mathbb{N}\] \[\to x^2 \leq x^2 + y^2 + z^2 = C\] \[x^2 \leq C\] \[|x| \leq \sqrt{C}\] \[-\sqrt{C} \leq x \leq \sqrt{C}\]
Lo mismo se cumple para \(y\) y \(z\). Además si tenemos \(x, y\), entonces
\(z = A - x - y\). De esta manera, podemos fijar \(x, y\) en \(O(\sqrt{C}^2) = O(C)\) y chequear si las ecuaciones se cumplen en \(O(1)\). No te olvides que \(x, y, z\) deben ser distintos.
Code
#include <bits/stdc++.h>
using namespace std;
void solve (int A, int B, int C) {
int lim = sqrt(C) + 1;
for (int x = -lim; x <= lim; x++) {
for (int y = -lim; y <= lim; y++) {
int z = A - x - y;
if (x == y or x == z or y == z) continue;
if ((x + y + z == A) and
(x * y * z == B) and
(x * x + y * y + z * z == C)) {
cout << x << ' ' << y << ' ' << z << '\n';
return;
}
}
}
cout << "No solution.\n";
}
int main () {
int tc;
cin >> tc;
while (tc--) {
int A, B, C;
cin >> A >> B >> C;
solve(A, B, C);
}
return (0);
}B: 2Char
2Char
La clave de este problema es darse cuenta cuál es el espacio de búsqueda. Como cada texto tendrá como máximo dos caracteres distintos y el máximo tamaño posible podemos fijar cuales serán los dos caracteres y solo tomar las cadenas que solo tengan esos caracteres.
Code
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 110;
int n, ans;
string word[MAX_N];
bool isValid (int id, char ch_1, char ch_2) {
for (int pos = 0; pos < word[id].size(); pos++) {
if (word[id][pos] != ch_1 and word[id][pos] != ch_2) {
return false;
}
}
return true;
}
int main () {
cin >> n;
for (int i = 0; i < n; i++) cin >> word[i];
for (char ch_1 = 'a'; ch_1 <= 'z'; ch_1++) {
for (char ch_2 = ch_1; ch_2 <= 'z'; ch_2++) {
int sum = 0;
for (int id = 0; id < n; id++) {
sum += isValid(id, ch_1, ch_2) * word[id].size();
}
ans = max(ans, sum);
}
}
cout << ans << endl;
return (0);
}C: Kaprekar Numbers
Kaprekar Numbers
Podemos preprocesar los números de Kaprekar en \([2, 40000]\) (solo hay 19 de ellos). Después podemos responder cada query buscando en esos 19 elementos.
Code
#include <bits/stdc++.h>
#define all(A) begin(A), end(A)
#define rall(A) rbegin(A), rend(A)
#define sz(A) int(A.size())
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long ll;
typedef pair <int, int> pii;
typedef vector <int> vi;
typedef vector <ll> vll;
const int N = 4e4;
vi kaprekar;
bool isKaprekar (int n) {
string sq = to_string(n * n);
for (int i = 0; i + 1 < sz(sq); i++) {
int l = stoi(sq.substr(0, i + 1));
int r = stoi(sq.substr(i + 1));
if (0 < min(l, r) and l + r == n) return true;
}
return false;
}
void preprocess () {
for (int n = 2; n <= N; n++) {
if (isKaprekar(n)) {
kaprekar.pb(n);
}
}
}
int main () {
ios::sync_with_stdio(false); cin.tie(0);
preprocess(); // just 19 elements
int tc;
cin >> tc;
for (int t = 1; t <= tc; t++) {
int l, r;
cin >> l >> r;
vi ans;
for (int elem: kaprekar) {
if (l <= elem and elem <= r) {
ans.pb(elem);
}
}
if (t > 1) cout << '\n';
cout << "case #" << t << '\n';
if (ans.empty()) {
cout << "no kaprekar numbers\n";
} else {
for (int elem: ans) {
cout << elem << '\n';
}
}
}
return (0);
}D: Ranges
Ranges
Primero, si tenemos esta suma:
\[l + (l + 1) + (l + 2) + \dots + (r - 1) + (r)\]
Podemos calcularla en \(O(1)\) usando esta fórmula:
\[\frac{r \cdot (r + 1)}{2} - \frac{(l - 1) \cdot l}{2}\]
Además, notamos que no podemos procesar cada consulta en \(O(N)\) (sino tendríamos una solución \(O(NQ)\) lo cual daría TLE), pero usando la anterior fórmula podemos responder cada consulta en \(O(U)\), así tenemos una solución en \(O(QU)\) lo cual es suficiente.
Code
#include <bits/stdc++.h>
#define all(A) begin(A), end(A)
#define rall(A) rbegin(A), rend(A)
#define sz(A) int(A.size())
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long ll;
typedef pair <int, int> pii;
typedef vector <int> vi;
typedef vector <ll> vll;
int main () {
ios::sync_with_stdio(false); cin.tie(0);
const ll MOD = 10000;
int n, u, q;
cin >> n >> u >> q;
vector <pii> update(u);
for (int i = 0; i < u; i++) cin >> update[i].first >> update[i].second;
auto get = [&] (ll x) {
return x * (x + 1) / 2;
};
while (q--) {
int l, r;
cin >> l >> r;
ll ans = 0;
for (auto pp: update) {
int L = max(pp.first, l);
int R = min(pp.second, r);
if (L <= R) {
ll x = L - pp.first + 1;
ll y = R - pp.first + 1;
ans += get(y) - get(x - 1);
ans %= MOD;
}
}
cout << ans << '\n';
}
return (0);
}E: Classroom Watch
Classroom Watch
Sea \(f(x) =\) suma de dígitos de \(x\).
Por los límites del problema tenemos que \(0 \leq f(x) \leq 9 \cdot 9\). Entonces, tenemos:
\[\max(0, n - 9 \cdot 9) \leq x \leq n\]
Así, nuestro espacio de búsqueda es muy pequeño, por lo que podemos simplemente hacer una búsqueda en ese intervalo.
Code
#include <bits/stdc++.h>
using namespace std;
int sumOfDigits (int p) {
int ret = 0;
while (p) ret += (p % 10), p /= 10;
return ret;
}
int main () {
int n;
vector <int> ans;
cin >> n;
for (int p = max(0, n - 9 * 9); p <= n; p++) if (p + sumOfDigits(p) == n) ans.push_back(p);
cout << ans.size() << endl;
for (auto x: ans) cout << x << endl;
return (0);
}F: Hyperset
Hyperset
Si fijamos dos cartas podemos determinar cual debe ser la tercera. Ten cuidado con la implementación.
Code
#include <bits/stdc++.h>
#define all(A) begin(A), end(A)
#define rall(A) rbegin(A), rend(A)
#define sz(A) int(A.size())
#define pb push_back
#define mp make_pair
using namespace std;
typedef unsigned long long ll;
typedef pair <int, int> pii;
int main () {
ios::sync_with_stdio(false); cin.tie(0);
int n, k;
cin >> n >> k;
vector <string> arr(n);
map <string, int> mp;
for (int i = 0; i < n; i++) {
cin >> arr[i], mp[arr[i]]++;
}
ll ans = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
string need = string(k, ' ');
for (int t = 0; t < k; t++) {
if (arr[i][t] == arr[j][t]) {
need[t] = arr[i][t];
} else {
if ('S' != arr[i][t] and 'S' != arr[j][t]) need[t] = 'S';
if ('E' != arr[i][t] and 'E' != arr[j][t]) need[t] = 'E';
if ('T' != arr[i][t] and 'T' != arr[j][t]) need[t] = 'T';
}
}
ans += mp[need];
}
}
cout << ans / 3 << '\n';
return (0);
}G: Get AC
Get AC
Podemos calcular cuando AC hay en un rango usando prefix sums y teniendo cuidando con los casos borde.
Code
#include <bits/stdc++.h>
#define all(A) begin(A), end(A)
#define sz(A) int(A.size())
using namespace std;
typedef long long ll;
int main () {
ios::sync_with_stdio(false); cin.tie(0);
int n, q;
cin >> n >> q;
string s;
cin >> s;
vector <int> ac(n + 1, 0);
for (int i = 1; i < n; i++) {
if (s[i - 1] == 'A' and s[i] == 'C') {
ac[i + 1] = 1;
}
}
for (int i = 1; i <= n; i++) {
ac[i] += ac[i - 1];
}
while (q--) {
int l, r;
cin >> l >> r;
int x = ac[r] - ac[l - 1];
if (ac[l] - ac[l - 1] == 1) x--;
cout << x << '\n';
}
return (0);
}